YEAR 7 MATHS FOCUS
NUMBER AND ALGEBRA
COMPUTATION WITH INTEGERS
OUTCOME
A student:
MA4-4NA:
compares, orders and calculates with integers, applying a range of strategies to aid computation
| TEACHING POINTS | To divide two- and three-digit numbers by a two-digit number, students may be taught the long division algorithm or, alternatively, to transform the division into a multiplication. So, 356÷52=□ becomes 52×□=356. Knowing that there are two fifties in each 100, students may try 7, obtaining 52 × 7 = 364, which is too large. They may then try 6, obtaining 52 × 6 = 312. The answer is 6 44/52=6 11/13 Students also need to be able to express a division in the following form in order to relate multiplication and division: 356 = 6 × 52 + 44, and then division by 52 gives 356/52=6+44/52=6 11/13 Students should have some understanding of integers, as the concept is introduced in Stage 3 Whole Numbers 2 (year 6). However, operations with integers are introduced in Stage 4. Complex recording formats for integers, such as raised signs, can be confusing. On printed materials, the en-dash ( – ) should be used to indicate a negative number and the operation of subtraction. The hyphen ( – ) should not be used in either context. The following formats are recommended: −2−3−7+(−4)−2−−3=−5=−7−4=−11=−2+3=1 Brahmagupta (c598–c665), an Indian mathematician and astronomer, is noted for the introduction of zero and negative numbers in arithmetic. |
| LANGUAGE | Teachers should model and use a variety of expressions for mathematical operations and should draw students’ attention to the fact that the words used for subtraction and division questions may require the order of the numbers to be reversed when performing the operation. For example, ‘9 take away 3’ and ‘reduce 9 by 3’ require the operation to be performed with the numbers in the same order as they are presented in the question (ie 9 – 3), but ‘take 9 from 3’, ‘subtract 9 from 3’ and ‘9 less than 3’ require the operation to be performed with the numbers in the reverse order to that in which they are stated in the question (ie 3 – 9). Similarly, ‘divide 6 by 2’ and ‘6 divided by 2’ require the operation to be performed with the numbers in the same order as they are presented in the question (ie 6 ÷ 2), but ‘how many 2s in 6?’ requires the operation to be performed with the numbers in the reverse order to that in which they appear in the question (ie 6 ÷ 2). |
| PURPOSE RELEVANCE OF SUBSTRAND | The positive integers (1, 2, 3, …) and 0 allow us to answer many questions involving ‘How many?’, ‘How much?’, ‘How far?’, etc, and so carry out a wide range of daily activities. The negative integers (…, –3, –2, –1) are used to represent ‘downwards’, ‘below’, ‘to the left’, etc, and appear in relation to everyday situations such as the weather (eg a temperature of –5° is 5° below zero), altitude (eg a location given as –20 m is 20 m below sea level), and sport (eg a golfer at –6 in a tournament is 6 under par). The Computation with Integers substrand includes the use of mental strategies, written strategies, etc to obtain answers – which are very often integers themselves – to questions or problems through addition, subtraction, multiplication and division. |
Expectations of Attainment
Apply the associative, commutative and distributive laws to aid mental and written computation (ACMNA151) | use an appropriate non-calculator method to divide two- and three-digit numbers by a two-digit number |
| – compare initial estimates with answers obtained by written methods and check by using a calculator {Problem Solving, Critical and creative thinking} | |
| show the connection between division and multiplication, including where there is a remainder, e.g. 451÷23=19 14/23 means that 451=19×23+14 {Critical and creative thinking} | |
| apply a practical understanding of commutativity to aid mental computation, e.g. 3 + 9 = 9 + 3 = 12, 3 × 9 = 9 × 3 = 27 {Critical and creative thinking} | |
| apply a practical understanding of associativity to aid mental computation, e.g. 3 + 8 + 2 = (3 + 8) + 2 = 3 + (8 + 2) = 13, 2 × 7 × 5 = (2 × 7) × 5 = 2 × (7 × 5) = 70 {Critical and creative thinking} | |
| – determine by example that associativity holds true for multiplication of three or more numbers but does not apply to calculations involving division, e.g. (80 ÷ 8) ÷ 2 is not equivalent to 80 ÷ (8 ÷ 2) {Communicating, Critical and creative thinking} | |
| apply a practical understanding of the distributive law to aid mental computation, e.g. to multiply any number by 13, first multiply by 10 and then add 3 times the number {Critical and creative thinking} | |
| use factors of a number to aid mental computation involving multiplication and division, e.g. to multiply a number by 12, first multiply the number by 6 and then multiply the result by 2 |
Compare, order, add and subtract integers (ACMNA280) | recognise and describe the ‘direction’ and ‘magnitude’ of integers |
| – construct a directed number sentence to represent a real-life situation {Communicating} | |
| recognise and place integers on a number line | |
| compare the relative value of integers, including recording the comparison by using the symbols < and > | |
| order integers | |
| interpret different meanings (direction or operation) for the + and – signs, depending on the context | |
| add and subtract integers using mental and written strategies | |
| – determine, by developing patterns or using a calculator, that subtracting a negative number is the same as adding a positive number {Reasoning, Critical and creative thinking} | |
| – apply integers to problems involving money and temperature {Problem Solving, Critical and creative thinking} |
Carry out the four operations with rational numbers and integers, using efficient mental and written strategies and appropriate digital technologies (ACMNA183) | multiply and divide integers using mental and written strategies |
| – investigate, by developing patterns or using a calculator, the rules associated with multiplying and dividing integers {Reasoning, Critical and creative thinking} | |
| use a calculator to perform the four operations with integers {Information and communication technology capability} | |
| – decide whether it is more appropriate to use mental strategies or a calculator when performing certain operations with integers {Communicating, Critical and creative thinking} | |
| use grouping symbols as an operator with integers | |
| apply the order of operations to mentally evaluate expressions involving integers, including where an operator is contained within the numerator or denominator of a fraction, e.g. (15+9)/6, (15+9)/(15−3), 5+(18−12)/6, 5+18/6−12, 5×(2−8) | |
| investigate whether different digital technologies, such as those found in computer software and on mobile devices, apply the order of operations {Problem Solving, Critical and creative thinking, Information and communication technology capability} |
FRACTIONS & DECIMALS
OUTCOME
A student:
MA4-5NA:
operates with fractions, decimals and percentages
| TEACHING POINTS | In Stage 3, the study of fractions is limited to denominators of 2, 3, 4, 5, 6, 8, 10, 12 and 100 and calculations involve related denominators only. Students are unlikely to have had any experience with rounding to a given number of decimal places prior to Stage 4. The term ‘decimal place’ may need to be clarified. Students should be aware that rounding is a process of ‘approximating’ and that a rounded number is an ‘approximation’. All recurring decimals are non-terminating decimals, but not all non-terminating decimals are recurring. The earliest evidence of fractions can be traced to the Egyptian papyrus of the scribe Ahmes (about 1650 BC). In the seventh century AD, the method of writing fractions as we write them now was invented in India, but without the fraction bar (vinculum), which was introduced by the Arabs. Fractions were widely in use by the twelfth century. One-cent and two-cent coins were withdrawn by the Australian Government in 1990. When an amount of money is calculated, it may have 1, 2, 3 or more decimal places, e.g. when buying petrol or making interest payments. When paying electronically, the final amount is paid correct to the nearest cent. When paying with cash, the final amount is rounded correct to the nearest five cents, eg $25.36, $25.37 round to $25.35 |
| LANGUAGE | In questions that require calculating a fraction or percentage of a quantity, some students may benefit from first writing an expression using the word ‘of’, before replacing it with the multiplication sign (×). When solving word problems, students should be encouraged to write a few key words on the left-hand side of the equals sign to identify what is being found in each step of their working. When expressing fractions in English, the numerator is said first, followed by the denominator. However, in many Asian languages (eg Chinese, Japanese), the opposite is the case: the denominator is said before the numerator. |
| PURPOSE RELEVANCE OF SUBSTRAND | There are many everyday situations where things, amounts or quantities are ‘fractions’ or parts (or ‘portions’) of whole things, whole amounts or whole quantities. Fractions are very important when taking measurements, such as when buying goods (eg three-quarters of a metre of cloth) or following a recipe (eg a third of a cup of sugar), when telling the time (eg a quarter past five), when receiving discounts while shopping (eg ‘half price’, ‘half off’), and when sharing a cake or pizza (eg ‘There are five of us, so we’ll get one-fifth of the pizza each’). ‘Decimals’ and ‘percentages’ represent different ways of expressing fractions (and whole numbers), and so are other ways of representing a part of a whole. Fractions (and decimals and percentages) are of fundamental importance in calculation, allowing us to calculate with parts of wholes and to express answers that are not whole numbers, e.g. 4÷5=45 (or 0.8 or 80%). |
Expectations of Attainment
Compare fractions using equivalence; locate and represent positive and negative fractions and mixed numerals on a number line (ACMNA152) | determine the highest common factor (HCF) of numbers and the lowest common multiple (LCM) of numbers |
| generate equivalent fractions | |
| write a fraction in its simplest form | |
| express improper fractions as mixed numerals and vice versa | |
| place positive and negative fractions, mixed numerals and decimals on a number line to compare their relative values | |
| – interpret a given scale to determine fractional values represented on a number line {Problem Solving} | |
| – choose an appropriate scale to display given fractional values on a number line, e.g. when plotting thirds or sixths, a scale of 3 cm for every whole is easier to use than a scale of 1 cm for every whole {Communicating, Reasoning} |
Solve problems involving addition and subtraction of fractions, including those with unrelated denominators (ACMNA153) | add and subtract fractions, including mixed numerals and fractions with unrelated denominators, using written and calculator methods |
| – recognise and explain incorrect operations with fractions, e.g. explain why 2/3+1/4≠3/7 {Communicating, Reasoning, Literacy, Critical and creative thinking} | |
| – interpret fractions and mixed numerals on a calculator display {Communicating, Critical and creative thinking} | |
| subtract a fraction from a whole number using mental, written and calculator methods, e.g. 3−2/3=2+1−2/3=2 1/3 |
Multiply and divide fractions and decimals using efficient written strategies and digital technologies (ACMNA154) | determine the effect of multiplying or dividing by a number with magnitude less than one |
| multiply and divide decimals by powers of 10 | |
| multiply and divide decimals using written methods, limiting operators to two digits | |
| – compare initial estimates with answers obtained by written methods and check by using a calculator {Problem Solving, Critical and creative thinking} | |
| multiply and divide fractions and mixed numerals using written methods | |
| – demonstrate multiplication of a fraction by another fraction using a diagram to illustrate the process {Communicating, Reasoning, Literacy} | |
| – explain, using a numerical example, why division by a fraction is equivalent to multiplication by its reciprocal {Communicating, Reasoning, Literacy, Critical and creative thinking} | |
| multiply and divide fractions and decimals using a calculator | |
| calculate fractions and decimals of quantities using mental, written and calculator methods | |
| – choose the appropriate equivalent form for mental computation, e.g. 0.25 of $60 is equivalent to 1/4 of $60, which is equivalent to $60 ÷ 4 {Communicating, Critical and creative thinking} |
Express one quantity as a fraction of another, with and without the use of digital technologies (ACMNA155) | express one quantity as a fraction of another |
| – choose appropriate units to compare two quantities as a fraction, e.g. 15 minutes is 15/60=1/4 of an hour {Communicating, Critical and creative thinking} |
Round decimals to a specified number of decimal places (ACMNA156) | round decimals to a given number of decimal places |
| use symbols for approximation, e.g. ≑ or ≈ {Literacy} |
Investigate terminating and recurring decimals(ACMNA184) | use the notation for recurring (repeating) decimals, e.g. 0.33333…=0.3˙, 0.345345345…=0.3˙45˙, 0.266666…=0.26˙ {Literacy} |
| convert fractions to terminating or recurring decimals as appropriate | |
| – recognise that calculators may show approximations to recurring decimals, and explain why, e.g. 23 displayed as 0.666666667 {Communicating, Reasoning, Critical and creative thinking} |
Connect fractions, decimals and percentages and carry out simple conversions (ACMNA157) | classify fractions, terminating decimals, recurring decimals and percentages as ‘rational’ numbers, as they can be written in the form ab where a and b are integers and b≠0 {Literacy} |
| convert fractions to decimals (terminating and recurring) and percentages | |
| convert terminating decimals to fractions and percentages | |
| convert percentages to fractions and decimals (terminating and recurring) | |
| – evaluate the reasonableness of statements in the media that quote fractions, decimals or percentages, e.g. ‘The number of children in the average family is 2.3’ {Communicating, Problem Solving, Critical and creative thinking} | |
| order fractions, decimals and percentages |
Investigate the concept of irrational numbers, including π (pie) (ACMNA186) | investigate ‘irrational’ numbers, such as π and √2 {Literacy Critical and creative thinking} |
| – describe, informally, the properties of irrational numbers {Communicating, Literacy} |
PERCENTAGES
OUTCOME
A student:
MA4-5NA:
operates with fractions, decimals and percentages
| TEACHING POINTS | One-cent and two-cent coins were withdrawn by the Australian Government in 1990. When an amount of money is calculated, it may have 1, 2, 3 or more decimal places, e.g. when buying petrol or making interest payments. When paying electronically, the final amount is paid correct to the nearest cent. When paying with cash, the final amount is rounded correct to the nearest five cents, eg $25.36, $25.37 round to $25.35 |
| LANGUAGE | In questions that require calculating a fraction or percentage of a quantity, some students may benefit from first writing an expression using the word ‘of’, before replacing it with the multiplication sign (×). Students may need assistance with the subtleties of the English language when solving word problems. The different processes required by the words ‘to’ and ‘by’ in questions such as ‘find the percentage increase if $2 is increased to $3’ and ‘find the percentage increase if $2 is increased by $3’ should be made explicit. When solving word problems, students should be encouraged to write a few key words on the left-hand side of the equals sign to identify what is being found in each step of their working. The word ‘cent’ is derived from the Latin word centum, meaning ‘one hundred’. ‘Percent’ means ‘out of one hundred’ or ‘hundredths’. |
| PURPOSE RELEVANCE OF SUBSTRAND | There are many everyday situations where things, amounts or quantities are ‘fractions’ or parts (or ‘portions’) of whole things, whole amounts or whole quantities. Fractions are very important when taking measurements, such as when buying goods (eg three-quarters of a metre of cloth) or following a recipe (eg a third of a cup of sugar), when telling the time (eg a quarter past five), when receiving discounts while shopping (eg ‘half price’, ‘half off’), and when sharing a cake or pizza (eg ‘There are five of us, so we’ll get one-fifth of the pizza each’). ‘Decimals’ and ‘percentages’ represent different ways of expressing fractions (and whole numbers), and so are other ways of representing a part of a whole. Fractions (and decimals and percentages) are of fundamental importance in calculation, allowing us to calculate with parts of wholes and to express answers that are not whole numbers, e.g. 4÷5=4/5 (or 0.8 or 80%). |
Expectations of Attainment
Connect fractions, decimals and percentages and carry out simple conversions (ACMNA157) | classify fractions, terminating decimals, recurring decimals and percentages as ‘rational’ numbers, as they can be written in the form ab where a and b are integers and b≠0 {Literacy} |
| convert fractions to decimals (terminating and recurring) and percentages | |
| convert terminating decimals to fractions and percentages | |
| convert percentages to fractions and decimals (terminating and recurring) | |
| – evaluate the reasonableness of statements in the media that quote fractions, decimals or percentages, e.g. ‘The number of children in the average family is 2.3’ {Communicating, Problem Solving, Critical and creative thinking} | |
| order fractions, decimals and percentages |
Find percentages of quantities and express one quantity as a percentage of another, with and without the use of digital technologies (ACMNA158) | calculate percentages of quantities using mental, written and calculator methods |
| choose an appropriate equivalent form for mental computation of percentages of quantities, e.g. 20% of $40 is equivalent to 1/5 × $40, which is equivalent to $40 ÷ 5 {Communicating, Critical and creative thinking} | |
| express one quantity as a percentage of another, using mental, written and calculator methods, e.g. 45 minutes is 75% of an hour |
Solve problems involving the use of percentages, including percentage increases and decreases, with and without the use of digital technologies (ACMNA187) | increase and decrease a quantity by a given percentage, using mental, written and calculator methods |
| – recognise equivalences when calculating percentage increases and decreases, e.g. multiplication by 1.05 will increase a number or quantity by 5%, multiplication by 0.87 will decrease a number or quantity by 13% {Reasoning} | |
| interpret and calculate percentages greater than 100, e.g. an increase from $2 to $5 is an increase of 150% | |
| solve a variety of real-life problems involving percentages, including percentage composition problems and problems involving money | |
| – interpret calculator displays in formulating solutions to problems involving percentages by appropriately rounding decimals {Communicating, Information and communication technology capability} | |
| – use the unitary method to solve problems involving percentages, e.g. find the original value, given the value after an increase of 20% {Problem Solving} | |
| – interpret and use nutritional information panels on product packaging where percentages are involved {Problem Solving, Literacy} | |
| – interpret and use media and sport reports involving percentages {Problem Solving, Critical and creative thinking} | |
| – interpret and use statements about the environment involving percentages, e.g. energy use for different purposes, such as lighting {Problem Solving, Critical and creative thinking, Sustainability} |
FINANCIAL MATHEMATICS
OUTCOME
A student:
MA4-6NA:
solves financial problems involving purchasing goods
| TEACHING POINTS | The Goods and Services Tax (GST) in Australia is a value-added tax on the supply of goods and services. It was introduced by the Australian Government and took effect from 1 July 2000. Prior to the GST, Australia operated a wholesale sales tax implemented in the 1930s, when its economy was dominated by the production and sale of goods. In Australia, the GST is levied at a flat rate of 10% on most goods and services, apart from GST-exempt items (which include basic necessities such as milk and bread). |
| LANGUAGE | GST stands for ‘Goods and Services Tax’. The difference between the GST-inclusive price, the pre-GST price, and the amount of the GST itself should be made explicit. When solving financial problems, students should be encouraged to write a few key words on the left-hand side of the equals sign to identify what is being found in each step of their working, and to conclude with a statement in words. Students’ understanding may be increased if they write calculations in words first, before substituting the appropriate values, e.g. percentage discount=discount/retail price×100% Students may need assistance with the subtleties of language used in relation to financial transactions, e.g. the difference between ‘$100 has been discounted by $10’ and ‘$100 has been discounted to $10’. |
| PURPOSE RELEVANCE | Financial mathematics’ is used in important areas relating to an individual’s daily financial transactions, money management, and financial decision making. Such areas include earning and spending money (eg calculating ‘best buys’, discounts, GST, personal taxation, profit and loss, investing money, credit and borrowing, hire purchase, simple and compound interest, loan repayments, and depreciation. |
Expectations of Attainment
Select and apply efficient mental and written strategies, and appropriate digital technologies, to solve problems involving multiplication and division with whole numbers (ACMNA123) | select and use efficient mental and written strategies, and digital technologies, to multiply whole numbers of up to four digits by one- and two-digit numbers |
| select and use efficient mental and written strategies, and digital technologies, to divide whole numbers of up to four digits by a one-digit divisor, including where there is a remainder | |
| – estimate solutions to problems and check to justify solutions {Problem Solving, Reasoning, Critical and creative thinking} | |
| use mental strategies to multiply and divide numbers by 10, 100, 1000 and their multiples | |
| solve word problems involving multiplication and division, e.g. ‘A recipe requires 3 cups of flour for 10 people. How many cups of flour are required for 40 people?’ {Critical and creative thinking} | |
| – use appropriate language to compare quantities, e.g. ‘twice as much as’, ‘half as much as’ {Communicating, Critical and creative thinking} | |
| – use a table or similar organiser to record methods used to solve problems {Communicating, Problem Solving, Information and communication technology capability} | |
| recognise symbols used to record speed in kilometres per hour, e.g. 80 km/h {Literacy} | |
| solve simple problems involving speed, e.g. ‘How long would it take to travel 600 km if the average speed for the trip is 75 km/h?’ {Critical and creative thinking} |
Explore the use of brackets and the order of operations to write number sentences (ACMNA134) | use the term ‘operations’ to describe collectively the processes of addition, subtraction, multiplication and division |
| investigate and establish the order of operations using real-life contexts, e.g. ‘I buy six goldfish costing $10 each and two water plants costing $4 each. What is the total cost?’; this can be represented by the number sentence 6 × 10 + 2 × 4 but, to obtain the total cost, multiplication must be performed before addition {Literacy, Critical and creative thinking, Work and enterprise} | |
| – write number sentences to represent real-life situations {Communicating, Problem Solving, Literacy} | |
| recognise that the grouping symbols ( ) and [ ] are used in number sentences to indicate operations that must be performed first {Literacy} | |
| recognise that if more than one pair of grouping symbols are used, the operation within the innermost grouping symbols is performed first | |
perform calculations involving grouping symbols without the use of digital technologies, (2+3)×(16−9)=5×7 3+[20÷(9−5)]=3+[20÷4]=3+5 | |
apply the order of operations to perform calculations involving mixed operations and grouping symbols, without the use of digital technologies, e.g. 32÷2×4=16×4 32÷(2×4)=32÷8 (32+2)×4=34×4 32+2×4=32+8 {Work and enterprise} | |
| – investigate whether different digital technologies apply the order of operations {Reasoning, Information and communication technology capability, Critical and creative thinking} | |
| recognise when grouping symbols are not necessary, eg 32 + (2 × 4) has the same answer as 32 + 2 × 4 |
RATIOS & RATES
OUTCOME
A student:
MA4-7NA:
operates with ratios and rates, and explores their graphical representation
TEACHING POINTS | In Stage 3 Fractions and Decimals, students study fractions with denominators of 2, 3, 4, 5, 6, 8, 10, 12 and 100. A unit fraction is any proper fraction in which the numerator is 1, eg 12, 13, 14, 15, … |
| The process of writing a fraction in its ‘simplest form’ involves reducing the fraction to its lowest equivalent form. In Stage 4, this is referred to as ‘simplifying’ a fraction. | |
| When subtracting mixed numerals, working with the whole-number parts separately from the fractional parts can lead to difficulties, particularly where the subtraction of the fractional parts results in a negative value, e.g. in the calculation of 2 1/3−1 5/6, 1/3−5/6 results in a negative value. |
LANGUAGE | Students should be able to communicate using the following language: whole, equal parts, half, quarter, eighth, third, sixth, twelfth, fifth, tenth, hundredth, thousandth, fraction, numerator, denominator, mixed numeral, whole number, number line, proper fraction, improper fraction, is equal to, equivalent, ascending order, descending order, simplest form, decimal, decimal point, digit, round to, decimal places, dollars, cents, best buy, percent, percentage, discount, sale price. |
| The decimal 1.12 is read as ‘one point one two’ and not ‘one point twelve’. | |
| The word ‘cent’ is derived from the Latin word centum, meaning ‘one hundred’. ‘Percent’ means ‘out of one hundred’ or ‘hundredths’. | |
| A ‘terminating’ decimal has a finite number of decimal places, eg 3.25 (2 decimal places), 18.421 (3 decimal places). |
Expectations of Attainment
Recognise and solve problems involving simple ratios (ACMNA173) | use ratios to compare quantities measured in the same units |
| write ratios using the : symbol, e.g. 4:7 {Literacy} | |
| – express one part of a ratio as a fraction of the whole, e.g. in the ratio 4:7, the first part is 4/11 of the whole {Communicating} | |
| simplify ratios, e.g. 4:6=2:3, 12:2=1:4, 0.3:1=3:10 | |
| apply the unitary method to ratio problems | |
| divide a quantity in a given ratio |
Solve a range of problems involving ratios and rates, with and without the use of digital technologies (ACMNA188) | interpret and calculate ratios that involve more than two numbers |
| solve a variety of real-life problems involving ratios, e.g. scales on maps, mixes for fuels or concrete | |
| use rates to compare quantities measured in different units | |
| – distinguish between ratios, where the comparison is of quantities measured in the same units, and rates, where the comparison is of quantities measured in different units | |
| convert given information into a simplified rate, e.g. 150 kilometres travelled in 2 hours = 75 km/h | |
| – solve a variety of real-life problems involving rates, including problems involving rate of travel {speed, Critical and creative thinking} |
Investigate, interpret and analyse graphs from authentic data (ACMNA180) | interpret distance/time graphs (travel graphs) made up of straight-line segments |
| – write or tell a story that matches a given distance/time graph {Communicating, Literacy} | |
| – match a distance/time graph to a description of a particular journey and explain the reasons for the choice {Communicating, Reasoning, Literacy} | |
| – compare distance/time graphs of the same situation, decide which one is the most appropriate, and explain why {Communicating, Reasoning, Literacy, Critical and creative thinking} | |
| recognise concepts such as change of speed and direction in distance/time graphs | |
| – describe the meaning of straight-line segments with different gradients in the graph of a particular journey {Communicating} | |
| – calculate speeds for straight-line segments of given distance/time graphs {Problem Solving} | |
| recognise the significance of horizontal line segments in distance/time graphs | |
| determine which variable should be placed on the horizontal axis in distance/time graphs | |
| draw distance/time graphs made up of straight-line segments | |
| sketch informal graphs to model familiar events, e.g. noise level during a lesson | |
| – record the distance of a moving object from a fixed point at equal time intervals and draw a graph to represent the situation, e.g. move along a measuring tape for 30 seconds using a variety of activities that involve a constant rate, such as walking forwards or backwards slowly, and walking or stopping for 10-second increments {Problem Solving} | |
| use the relative positions of two points on a line graph, rather than a detailed scale, to interpret information |
ALGEBRAIC TECHNIQUES
OUTCOME
A student:
MA4-8NA:
generalises number properties to operate with algebraic expressions
| TEACHING POINTS | It is important to develop an understanding of the use of pronumerals (letters) as algebraic symbols to represent one or more numerical values. The recommended approach is to spend time on the conventions for the use of algebraic symbols for first-degree expressions and to situate the translation of generalisations from words to symbols as an application of students’ knowledge of the symbol system, rather than as an introduction to the symbol system. The recommended steps for moving into symbolic algebra are: the variable notion, associating letters with a variety of different numerical values; symbolism for a pronumeral plus a constant; symbolism for a pronumeral times a constant; symbolism for sums, differences, products and quotients. So, if a=6, a+a=6+6, but 2a=2×6 and not 26. To gain an understanding of algebra, students must be introduced to the concepts of pronumerals, expressions, unknowns, equations, patterns, relationships and graphs in a wide variety of contexts. For each successive context, these ideas need to be redeveloped. Students need gradual exposure to abstract ideas as they begin to relate algebraic terms to real situations. It is suggested that the introduction of representation through the use of algebraic symbols precede Linear Relationships in Stage 4, since this substrand presumes that students are able to manipulate algebraic symbols and will use them to generalise patterns. |
| LANGUAGE | For the introduction of algebra in Stage 4, the term ‘pronumeral’ rather than ‘variable’ is preferred when referring to unknown numbers. In an algebraic expression such as 2x+5,x can take any value (ie x is variable and a pronumeral). However, in an equation such as 2x+5=11,x represents one particular value (ie x is not a variable but is a pronumeral). In equations such as x+y=11, x and y can take any values that sum to 11 (ie x and y are variables and pronumerals). ‘Equivalent’ is the adjective for ‘equal’, although ‘equal’ can also be used as an adjective, ie ‘equivalent expressions’ or ‘equal expressions’. Some students may confuse the order in which terms or numbers are to be used when a question is expressed in words. This is particularly apparent for word problems that involve subtraction or division to obtain the required result, e.g. ‘5x less than x’ and ‘take 5x from x’ both require the order of the terms to be reversed to x−5x in the solution. Students need to be familiar with the terms ‘sum’, ‘difference’, ‘product’ and ‘quotient’ to describe the results of adding, subtracting, multiplying and dividing, respectively. |
| PURPOSE RELEVANCE | Algebra is used to some extent throughout our daily lives. People are solving equations (usually mentally) when, for example, they are working out the right quantity of something to buy, or the right amount of an ingredient to use when adapting a recipe. Algebra requires, and its use results in, learning how to apply logical reasoning and problem-solving skills. It is used more extensively in other areas of mathematics, the sciences, business, accounting, etc. The widespread use of algebra is readily seen in the writing of formulas in spreadsheets. |
Expectations of Attainment
Introduce the concept of variables as a way of representing numbers using letters (ACMNA175) | develop the concept that pronumerals (letters) can be used to represent numerical values |
| – recognise that pronumerals can represent one or more numerical values (when more than one numerical value, pronumerals may then be referred to as ‘variables’) {Communicating, Reasoning, Literacy} | |
| model the following using concrete materials or otherwise: – expressions that involve a pronumeral, and a pronumeral added to a constant, e.g. a, a+1 – expressions that involve a pronumeral multiplied by a constant, e.g. 2a, 3a – sums and products, e.g. 2a+1, 2(a+1) – equivalent expressions, e.g. x+x+y+y+3=2x+2y+3=2(x+y)+3 – simplifying expressions, e.g. (a+2)+(2a+3)=(a+2a)+(2+3)=3a+5 | |
| recognise and use equivalent algebraic expressions, e.g. y+y+y+y=4y w×w=w^2 a×b=ab a÷b=a/b {Literacy} | |
| use algebraic symbols to represent mathematical operations written in words and vice versa, e.g. the product of x and y is xy, x+y is the sum of x and y {Literacy} |
Extend and apply the laws and properties of arithmetic to algebraic terms and expressions (ACMNA177) | recognise like terms and add and subtract them to simplify algebraic expressions, e.g. 2n+4m+n=4m+3n |
| – verify whether a simplified expression is correct by substituting numbers for pronumerals {Communicating, Reasoning} | |
| – connect algebra with the commutative and associative properties of arithmetic to determine that a+b=b+a and (a+b)+c=a+(b+c) {Communicating, Critical and creative thinking} | |
| recognise the role of grouping symbols and the different meanings of expressions, such as 2a+1 and 2(a+1) {Critical and creative thinking} | |
| simplify algebraic expressions that involve multiplication and division, e.g. 12a÷3, 4x×3, 2ab×3a, (8a)/2, (2a)/8, (12a)/9 | |
| – recognise the equivalence of algebraic expressions involving multiplication, e.g. 3bc=3cb {Communicating, Critical and creative thinking} | |
| – connect algebra with the commutative and associative properties of arithmetic to determine that a×b=b×a and (a×b)×c=a×(b×c) {Communicating, Critical and creative thinking} | |
| – recognise whether particular algebraic expressions involving division are equivalent or not, e.g. a÷bc is equivalent to a/bc and a÷(b×c), but is not equivalent to a÷b×c or a/b×c {Communicating, Critical and creative thinking} | |
| translate from everyday language to algebraic language and vice versa {Literacy} | |
| – use algebraic symbols to represent simple situations described in words, e.g. write an expression for the number of cents in x dollars {Communicating, Literacy} | |
| – interpret statements involving algebraic symbols in other contexts, e.g. cell references when creating and formatting spreadsheets {Communicating, Literacy, Information and communication technology capability} |
Simplify algebraic expressions involving the four operations (ACMNA192) | simplify a range of algebraic expressions, including those involving mixed operations |
| apply the order of operations to simplify algebraic expressions {Problem Solving} |
INDICES
OUTCOME
A student:
MA4-9NA:
- operates with positive-integer and zero indices of numerical bases
| TEACHING POINTS | Students have not used indices prior to Stage 4 and so the meaning and use of index notation will need to be made explicit. However, students should have some experience from Stage 3 in multiplying more than two numbers together at the same time. In Stage 3, students used the notion of factorising a number as a mental strategy for multiplication. Teachers may like to make an explicit link to this in the introduction of the prime factorisation of a number in Stage 4, e.g. in Stage 3, 18×5 The square root sign signifies a positive number (or zero). So, √9=3 (only). However, the two numbers whose square is 9 are √9 and −√9, i.e. 3 and –3. |
| LANGUAGE | Students need to be able to express the concept of divisibility in different ways, such as ’12 is divisible by 2′, ‘2 divides (evenly) into 12’, ‘2 goes into 12 (evenly)’. A ‘product of prime factors’ can also be referred to as a ‘product of primes’. Students are introduced to indices in Stage 4. The different expressions used when referring to indices should be modelled by teachers. Teachers should use fuller expressions before shortening them, e.g. 2^4 should be expressed as ‘2 raised to the power of 4’, before ‘2 to the power of 4’ and finally ‘2 to the 4’. Students are expected to use the words ‘squared’ and ‘cubed’ when saying expressions containing indices of 2 and 3, respectively, e.g. 4^2 is ‘four squared’, 4^3 is ‘four cubed’. Words such as ‘product’, ‘prime’, ‘power’, ‘base’ and ‘index’ have different meanings outside of mathematics. Words such as ‘base’, ‘square’ and ‘cube’ also have different meanings within mathematics, e.g. ‘the base of the triangle’ versus ‘the base of 3^2 |
| PURPOSE RELEVANCE | Indices are important in mathematics and in everyday situations. Among their most significant uses is that they allow us to write large and small numbers more simply, and to perform calculations with large and small numbers more easily. For example, without the use of indices, 21000 would be written as 2×2×2×2…, until ‘2’ appeared exactly 1000 times. |
Expectations of Attainment
Investigate index notation and represent whole numbers as products of powers of prime numbers (ACMNA149) | describe numbers written in ‘index form’ using terms such as ‘base’, ‘power’, ‘index’, ‘exponent’ {Literacy} |
| use index notation to express powers of numbers (positive indices only), e.g. 8=23 {Literacy} | |
| evaluate numbers expressed as powers of integers, e.g. 2^3=8, (−2)^3=−8 | |
| – investigate and generalise the effect of raising a negative number to an odd or even power on the sign of the result {Communicating, Critical and creative thinking} | |
| apply the order of operations to evaluate expressions involving indices, with and without using a calculator, e.g. 3^2+4^2, 4^3+2×5^2 {Information and communication technology capability} | |
| determine and apply tests of divisibility for 2, 3, 4, 5, 6 and 10 {Critical and creative thinking} | |
| – verify the various tests of divisibility using a calculator {Problem Solving, Information and communication technology capability} | |
| – apply tests of divisibility mentally as an aid to calculation {Problem Solving, Critical and creative thinking} | |
| express a number as a product of its prime factors, using index notation where appropriate | |
| – recognise that if a given number is divisible by a composite number, then it is also divisible by the factors of that number, e.g. since 660 is divisible by 6, then 660 is also divisible by factors of 6, which are 2 and 3 {Reasoning, Critical and creative thinking} | |
| – find the highest common factor of large numbers by first expressing the numbers as products of prime factors {Communicating, Problem Solving, Critical and creative thinking} |
Investigate and use square roots of perfect square numbers (ACMNA150) | use the notations for square root {Literacy} |
| recognise the link between squares and square roots and between cubes and cube roots, e.g. 2^3=8 and ^3√8=2 {Critical and creative thinking} | |
| determine through numerical examples that: | |
| express a number as a product of its prime factors to determine whether its square root and/or cube root is an integer | |
| find square roots and cube roots of any non-square whole number using a calculator, after first estimating {Information and communication technology capability} | |
| – determine the two integers between which the square root of a non-square whole number lies {Reasoning, Critical and creative thinking} | |
apply the order of operations to evaluate expressions involving square roots and cube roots, with and without using a calculator, e.g. Figure 2 {Information and communication technology capability} | |
explain the difference between pairs of numerical expressions that appear similar, e.g. ‘Is √36+√64 equivalent to √36+64 ?’ |
Use index notation with numbers to establish the index laws with positive-integer indices and the zero index (ACMNA182) | develop index laws with positive-integer indices and numerical bases by expressing each term in expanded form, e.g. Figure 3 {Literacy} |
| – verify the index laws using a calculator, e.g. use a calculator to compare the values of (3^4)^2 and 3^8 {Reasoning} | |
| – explain the incorrect use of index laws, e.g. explain why 3^2×3^4≠9^6 {Communicating, Reasoning, Literacy, Critical and creative thinking} | |
establish the meaning of the zero index, e.g. by patterns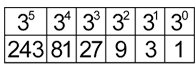 {Critical and creative thinking} | |
| – verify the zero index law using a calculator {Reasoning, Information and communication technology capability} | |
| use index laws to simplify expressions with numerical bases, e.g. 5^2×5^4×5=5^7 |
EQUATIONS
OUTCOME
A student:
MA4-10NA:
- operates with positive-integer and zero indices of numerical bases
INDICES
OUTCOME
A student:
MA4-9NA:
- operates with positive-integer and zero indices of numerical bases
| TEACHING POINTS | The solution of simple equations can be introduced using a variety of models. Such models include using a two-pan balance with objects such as centicubes and a wrapped ‘unknown’, or using some objects hidden in a container as an ‘unknown’ to produce a number sentence. The solution of simple quadratic equations in Stage 4 enables students to determine side lengths in right-angled triangles through the application of Pythagoras’ theorem. |
| LANGUAGE | Describing the steps in the solution of equations provides students with the opportunity to practise using mathematical imperatives in context, e.g. ‘add 5 to both sides’, ‘increase both sides by 5’, ‘subtract 3 from both sides’, ‘take 3 from both sides’, ‘decrease both sides by 3’, ‘reduce both sides by 3’, ‘multiply both sides by 2’, ‘divide both sides by 2’. |
| PURPOSE RELEVANCE | An equation is a statement that two quantities or expressions are equal, usually through the use of numbers and/or symbols. Equations are used throughout mathematics and in our daily lives in obtaining solutions to problems of all levels of complexity. People are solving equations (usually mentally) when, for example, they are working out the right quantity of something to buy, or the right amount of an ingredient to use when adapting a recipe. |
Expectations of Attainment
Solve simple linear equations (ACMNA179) | distinguish between algebraic expressions where pronumerals are used as variables, and equations where pronumerals are used as unknowns {Critical and creative thinking} |
| solve simple linear equations using concrete materials, such as the balance model or cups and counters, stressing the notion of performing the same operation on both sides of an equation | |
solve linear equations that may have non-integer solutions, using algebraic techniques that involve up to two steps in the solution process, e.g.
| |
| – compare and contrast strategies to solve a variety of linear equations {Communicating, Reasoning, Critical and creative thinking} | |
| – generate equations with a given solution, e.g. find equations that have the solution x=5 {Problem Solving} |
Solve linear equations using algebraic techniques and verify solutions by substitution (ACMNA194) | solve linear equations that may have non-integer solutions, using algebraic techniques that involve up to three steps in the solution process, e.g. Figure 7 |
| check solutions to equations by substituting {Critical and creative thinking} |
Solve simple quadratic equations | determine that if c>0 then there are two values of x that solve a simple quadratic equation of the form x^2=c |
| – explain why quadratic equations could be expected to have two solutions {Communicating, Reasoning, Critical and creative thinking} | |
| – recognise that x^2=c does not have a solution if c is a negative number {Communicating, Reasoning, Critical and creative thinking} | |
| solve simple quadratic equations of the form x^2=c, leaving answers in ‘exact form’ and as decimal approximations |
OUTCOME
A student:
MA4-11NA:
- creates and displays number patterns; graphs and analyses linear relationships; and performs transformations on the Cartesian plane
| TEACHING POINTS | When describing number patterns algebraically, it is important that students develop an understanding of the use of pronumerals as algebraic symbols for numbers of objects rather than for the objects themselves. In Linear Relationships, the study of patterns focuses on those that are linear. However, teachers may include a few simple non-linear patterns so that students realise that not all patterns are linear. The Cartesian plane (commonly referred to as the ‘number plane’) is named after the French philosopher and mathematician René Descartes (1596–1650), who was one of the first to develop analytical geometry on the number plane. On the Cartesian plane, the coordinates of a point refer to an ordered pair (x,y) describing the horizontal position x first, followed by the vertical position y. Students are introduced to the four quadrants of the Cartesian plane in Stage 3. However, they may not be familiar with the terms ‘Cartesian plane’, ‘x-axis’ and ‘y-axis’, as in Stage 3 these are generally referred to as the ‘number plane’, ‘horizontal axis’ and ‘vertical axis’, respectively. |
| LANGUAGE | In Stage 3, students were introduced to patterns involving one operation and used the terms ‘position in the pattern’ and ‘value of the term’ when describing a rule for a pattern from a table of values, eg ‘The value of the term is three times the position in the pattern’. Students will need to become familiar with and be able to use new terms, including ‘coefficient’, ‘constant term’ and ‘intercept’. Students should be aware that ‘gradient’ may be referred to as ‘slope’ in some contexts. |
| PURPOSE RELEVANCE | Linear relationships are very common in mathematics and science. The graph of two quantities that have a linear relationship is a straight line. A linear relationship may be a direct relationship or an inverse relationship. In a direct relationship, as one quantity increases, the other quantity also increases, or as one quantity decreases, the other quantity also decreases. In an inverse relationship, as one quantity increases, the other quantity decreases. Examples of linear relationships familiar in everyday life include the distance travelled and time taken, the conversion of one currency to another, the cost of printing involving an initial set-up cost and a dollar rate per item, the cost of taxi fares involving a hiring charge and a dollar rate per kilometre, and the cost of catering involving a base amount for a set number of people plus a rate for each extra attendee. Coordinate geometry facilitates the exploration and interpretation of linear relationships. |
| Given coordinates, plot points on the Cartesian plane, and find coordinates for a given point (ACMNA178) | plot and label points on the Cartesian plane, given coordinates, including those with coordinates that are not whole numbers |
| identify and record the coordinates of given points on the Cartesian plane, including those with coordinates that are not whole numbers |
| Describe translations, reflections in an axis, and rotations of multiples of 90° on the Cartesian plane using coordinates (ACMMG181) | use the notation P′ to name the ‘image’ resulting from a transformation of a point P on the Cartesian plane |
| plot and determine the coordinates for P′ resulting from translating P one or more times | |
plot and determine the coordinates for P′ resulting from reflecting P in either the x or -axis
| |
plot and determine the coordinates for P resulting from rotating P by a multiple of 90° about the origin
|
| Plot linear relationships on the Cartesian plane, with and without the use of digital technologies (ACMNA193) | use objects to build a geometric pattern, record the results in a table of values, describe the pattern in words and algebraic symbols, and represent the relationship on a number grid, eg
check pattern descriptions by substituting further values (Reasoning)
|
recognise a given number pattern (including decreasing patterns), complete a table of values, describe the pattern in words and algebraic symbols, and represent the relationship on a number grid
| |
| use a rule generated from a pattern to calculate the corresponding value for a larger number | |
form a table of values for a linear relationship by substituting a set of appropriate values for either of the pronumerals and graph the number pairs on the Cartesian plane, eg given y = 3x + 1, form a table of values using x = 0, 1 and 2 and then graph the number pairs on the Cartesian plane with an appropriate scale
| |
extend the line joining a set of points on the Cartesian plane to show that there is an infinite number of ordered pairs that satisfy a given linear relationship
| |
| derive a rule for a set of points that has been graphed on the Cartesian plane | |
graph more than one line on the same set of axes using digital technologies and compare the graphs to determine similarities and differences, eg parallel, pass through the same point
y=3x, y=3x+2, y=3x−2 y=x, y=2x, y=3x y=−x, y=x
| |
use digital technologies to graph linear and simple non-linear relationships, such as y=x2
|
| Solve linear equations using graphical techniques | recognise that each point on the graph of a linear relationship represents a solution to a particular linear equation |
| use graphs of linear relationships to solve a corresponding linear equation, with and without the use of digital technologies, eg use the graph of y = 2x + 3 to find the solution of the equation 2x + 3 = 11 | |
graph two intersecting lines on the same set of axes and read off the point of intersection
|
MEASUREMENT AND GEOMETRY
LENGTH
OUTCOME
A student:
MA4-12MG:
- calculates the perimeters of plane shapes and the circumferences of circles
TEACHING POINTS | Students should develop a sense of the levels of accuracy that are appropriate to a particular situation, eg the length of a bridge may be measured in metres to estimate a quantity of paint needed, but would need to be measured much more accurately for engineering work. |
| The number π is known to be irrational (not a fraction) and also transcendental (not the solution of any polynomial equation with integer coefficients). In Stage 4, students only need to know that the digits in its decimal expansion do not repeat (all this means is that it is not a fraction) and in fact have no known pattern. |
| RELEVANCE | This substrand focuses on the ‘perimeter’ (or length of the boundary) of shapes (including the ‘circumference’ of a circle). The ability to determine the perimeters of two-dimensional shapes is of fundamental importance in many everyday situations, such as framing a picture, furnishing a room, fencing a garden or a yard, and measuring land for farming or building construction. |
| LANGUAGE | Pi (π) is the Greek letter equivalent to ‘p’ and is the first letter of the Greek word perimetron, meaning ‘perimeter’. The symbol for pi was first used to represent the ratio of the circumference to the diameter of a circle in the early eighteenth century. The names for some parts of the circle (centre, radius, diameter, circumference, sector, semicircle and quadrant) are introduced in Stage 3. The terms ‘arc’, ‘tangent’, ‘chord’ and ‘segment’ are introduced in Stage 4. Some students may find the use of the terms ‘length/long’, ‘breadth/broad’, ‘width/wide’ and ‘height/high’ difficult. Teachers should model the use of these terms in sentences, both verbally and in written form, when describing diagrams. Students should be encouraged to speak about, listen to, read about and write about the dimensions of given shapes using various combinations of these words, eg ‘The length of this rectangle is 7 metres and the width is 4 metres’, ‘The rectangle is 7 metres long and 4 metres wide’. Students may also benefit from drawing and labelling a shape, given a description of its features in words, eg ‘The base of an isosceles triangle is 6 metres long and its perimeter is 20 metres. Draw the triangle and mark on it the lengths of the three sides’. In Stage 3, students were introduced to the term ‘dimensions’ to describe the length and width of a rectangle. However, some students may need to be reminded of this. |
Expectations of Attainment
| Find perimeters of parallelograms, trapeziums, rhombuses and kites (ACMMG196) | find the perimeters of a range of plane shapes, including parallelograms, trapeziums, rhombuses, kites and simple composite figures compare perimeters of rectangles with the same area (Problem Solving) |
| solve problems involving the perimeters of plane shapes, eg find the dimensions of a rectangle, given its perimeter and the length of one side |
| Investigate the concept of irrational numbers, including π (ACMNA186) | demonstrate by practical means that the ratio of the circumference to the diameter of a circle is constant, eg measure and compare the diameters and circumferences of various cylinders or use dynamic geometry software to measure circumferences and diameters |
define the number π as the ratio of the circumference to the diameter of any circleLiteracy
|
| Investigate the relationship between features of circles, such as the circumference, radius and diameter; use formulas to solve problems involving circumference (ACMMG197) | identify and name parts of a circle and related lines, including arc, tangent, chord, sector and segment |
develop and use the formulas to find the circumferences of circles in terms of the diameter d or radius r:
| |
find the perimeters of quadrants and semicircles | |
find the perimeters of simple composite figures consisting of two shapes, including quadrants and semicircles | |
find arc lengths and the perimeters of sectors | |
solve a variety of practical problems involving circles and parts of circles, giving an exact answer in terms of π and an approximate answer using a calculator’s approximation for π |
AREA
OUTCOME
A student:
MA4-13MG:
- uses formulas to calculate the areas of quadrilaterals and circles, and converts between units of area
TEACHING POINTS | The area formulas for the triangle, the special quadrilaterals and the circle should be developed by practical means and/or by the use of dynamic geometry software, such as prepared applets. |
| The area formulas for the triangle and the parallelogram should be related to the area of a rectangle. Applets may be particularly useful in demonstrating that the respective formulas hold for all triangles and parallelograms, including those for which the perpendicular height needs to be drawn outside the shape. | |
| The area formula for the rhombus or kite depends upon the fact that the diagonals are perpendicular, and so is linked with the geometry of special quadrilaterals. The formula applies to any quadrilateral in which the diagonals are perpendicular. Students should also be aware that because the rhombus is a special type of parallelogram, the area can be found using the formula A=bh. | |
| The area formula for the trapezium can be developed using various dissections and techniques. Students need to be able to apply the area formula for the trapezium appropriately to trapeziums in any form or orientation. | |
| The area formula for the circle may be established by using one or both of the following dissections: cut a circle into a large number of sectors and arrange the sectors alternately point-up and point-down to form a rectangle with height r and base length πr; inscribe a number of congruent triangles in a circle, all with corresponding vertex at the centre, and show that the area of the inscribed polygon is half the length of the perimeter times the perpendicular height of the triangles. | |
| Students should be made aware that the perpendicular height of a triangle is the shortest distance from the base to the opposite angle. They may also need to be explicitly taught that the shortest distance between the parallel sides of a quadrilateral is the perpendicular distance between these sides. | |
| Finding the areas of rectangles and squares with integer side lengths is an important link between geometry and multiplying, dividing, factoring and squaring. Expressing a number as the product of two of its factors is equivalent to forming a rectangle with those factors as the side lengths, and (where possible) expressing a number as the square of one of its factors is equivalent to forming a square with that factor as the side length. | |
| Graphing the relationship between the length of a rectangle with a constant perimeter and possible areas of the rectangle links to non-linear graphs. |
| LANGUAGE | Teachers should reinforce with students the use of the term ‘perpendicular height’, rather than simply ‘height’, when referring to this attribute of a triangle. Students should also benefit from drawing and labelling a triangle when given a description of its features in words. Students may improve their understanding and retention of the area formulas by expressing them in different ways, eg ‘The area of a trapezium is half the perpendicular height multiplied by the sum of the lengths of the parallel sides’, ‘The area of a trapezium is half the product of the perpendicular height and the sum of the lengths of the parallel sides’. The use of the term ‘respectively’ in measurement word problems should be modelled and the importance of the order of the words explained, eg in the sentence ‘The perpendicular height and base of a triangle are 5 metres and 8 metres, respectively’, the first attribute (perpendicular height) mentioned refers to the first measurement (5 metres), and so on. The abbreviation m2 is read as ‘square metre(s)’ and not ‘metre(s) squared’ or ‘metre(s) square’. Similarly, the abbreviation cm2 is read as ‘square centimetre(s)’ and not ‘centimetre(s) squared’ or ‘centimetre(s) square’. When units are not provided in an area question, students should record the area in ‘square units’. |
EXPECTATIONS OF ATTAINMENT
| Choose appropriate units of measurement for area and convert from one unit to another | choose an appropriate unit to measure the areas of different shapes and surfaces, eg floor space, fieldsCritical and creative thinking
|
| convert between metric units of area using 1 cm2 = 100 mm2, 1 m2 = 1 000 000 mm2, 1 ha = 10 000 m2, 1 km2 = 1 000 000 m2 = 100 ha |
Establish the formulas for areas of rectangles, triangles and parallelograms and use these in problem solving | develop and use the formulas to find the areas of rectangles and squares: Area of rectangle=lb where l is the length and b is the breadth (or width) of the rectangle
|
| find the areas of simple composite figures that may be dissected into rectangles, squares, parallelograms and triangles |
Find areas of trapeziums, rhombuses and kites
| develop, with or without the use of digital technologies, and use the formula to find the areas of kites and rhombuses: |
develop and use the formula to find the areas of trapeziums:
| |
select and use the appropriate formula to find the area of any of the special quadrilaterals | |
solve a variety of practical problems relating to the areas of triangles and quadrilaterals
|
Investigate the relationship between features of circles, such as the area and the radius; use formulas to solve problems involving area
| develop, with or without the use of digital technologies, and use the formula to find the areas of circles: Area of circle=πr2 where r is the length of the radius
|
find the areas of quadrants, semicircles and sectors | |
solve a variety of practical problems involving circles and parts of circles, giving an exact answer in terms of π and an approximate answer using a calculator’s approximation for π |
VOLUME & CAPACITY
OUTCOME
A student:
MA4-14MG:
uses formulas to calculate the volumes of prisms and cylinders, and converts between units of volume
TEACHING POINTS | When developing the volume formula for a prism, students require an understanding of the idea of a uniform cross-section and should visualise, for example, stacking unit cubes, layer by layer, into a rectangular prism, or stacking planks into a pile. In the formula for the volume of a prism, V=Ah, A refers to the ‘area of the base’, which can also be referred to as the ‘area of the uniform cross-section’. |
| ‘Oblique’ prisms, cylinders, pyramids and cones are those that are not ‘right’ prisms, cylinders, pyramids and cones, respectively. The focus here is on right prisms and cylinders, although the formulas for volume also apply to oblique prisms and cylinders provided that the perpendicular height is used. In a right prism, the base and top are perpendicular to the other faces. In a right pyramid or cone, the base has a centre of rotation, and the interval joining that centre to the apex is perpendicular to the base (and therefore is its axis of rotation). | |
| The volumes of rectangular prisms and cubes are linked with multiplication, division, powers and factorisation. Expressing a number as the product of three of its factors is equivalent to forming a rectangular prism with those factors as the side lengths, and (where possible) expressing a number as the cube of one of its factors is equivalent to forming a cube with that factor as the side length. | |
| The abbreviation for megalitres is ML. Students will need to be careful not to confuse this with the abbreviation mL used for millilitres. |
| RELEVANCE | The ability to determine the volumes of three-dimensional objects and the capacities of containers, and to solve related problems, is of fundamental importance in many everyday activities, such as calculating the number of cubic metres of concrete, soil, sand, gravel, mulch or other materials needed for building or gardening projects; the amount of soil that needs to be removed for the installation of a swimming pool; and the appropriate size in litres of water tanks and swimming pools. |
Knowledge and understanding with regard to determining the volumes of simple three-dimensional objects (including containers) such as cubes, other rectangular prisms, triangular prisms, cylinders, pyramids, cones and spheres can be readily applied to determining the volumes and capacities of composite objects (including containers). |
LANGUAGE | The word ‘base’ may cause confusion for some students. The ‘base’ in relation to two-dimensional shapes is linear, whereas in relation to three-dimensional objects, ‘base’ refers to a surface. In everyday language, the word ‘base’ is used to refer to that part of an object on, or closest to, the ground. In the mathematics of three-dimensional objects, the term ‘base’ is used to describe the face by which a prism or pyramid is named, even though it may not be the face on, or closest to, the ground. Students should be aware that a cube is a special prism that has six congruent faces. |
The abbreviation m3 is read as ‘cubic metre(s)’ and not ‘metre(s) cubed’ or ‘metre(s) cube’. When units are not provided in a volume question, students should record the volume in ‘cubic units’. |
EXPECTATIONS OF ATTAINMENT
| Draw different views of prisms and solids formed from combinations of prisms (ACMMG161) | draw (in two dimensions) prisms, and solids formed from combinations of prisms, from different views, including top, side, front and back views |
identify and draw the cross-sections of different prismsLiteracy Critical and creative thinking
| |
| visualise, construct and draw various prisms from a given cross-sectional diagram | |
determine if a particular solid has a uniform cross-sectionCritical and creative thinking
|
| Choose appropriate units of measurement for volume and convert from one unit to another (ACMMG195) | recognise that 1000 litres is equal to one kilolitre and use the abbreviation for kilolitres (kL) |
| ecognise that 1000 kilolitres is equal to one megalitre and use the abbreviation for megalitres (ML) | |
choose an appropriate unit to measure the volumes or capacities of different objects, eg swimming pools, household containers, damsLiteracy Sustainability
| |
| convert between metric units of volume and capacity, using 1 cm3 = 1000 mm3, 1 L = 1000 mL = 1000 cm3, 1 m3 = 1000 L = 1 kL, 1000 kL = 1 ML |
| Develop the formulas for the volumes of rectangular and triangular prisms and of prisms in general; use formulas to solve problems involving volume (ACMMG198) | develop the formula for the volume of prisms by considering the number and volume of ‘layers’ of identical shape:
|
| find the volumes of prisms, given their perpendicular heights and the areas of their uniform cross-sections | |
| find the volumes of prisms with uniform cross-sections that are rectangular or triangular | |
| solve a variety of practical problems involving the volumes and capacities of right prisms |
| Calculate the volumes of cylinders and solve related problems (ACMMG217) | develop and use the formula to find the volumes of cylinders:
|
| solve a variety of practical problems involving the volumes and capacities of right prisms and cylinders, eg find the capacity of a cylindrical drink can or a water tank |
TIME
OUTCOME
A student:
MA4-15MG:
performs calculations of time that involve mixed units, and interprets time zones
TEACHING POINTS | Calculations involving time can be made on a scientific calculator either by using fractions and decimals or by using the ‘degrees, minutes, seconds’ button. Students should be familiar with both approaches. |
| Typically, 24-hour time is recorded without the use of the colon (:), e.g. 3:45 pm is written as 1545 or 1545 h and read as ‘fifteen forty-five hours’. |
| RELEVANCE | The relevance of this substrand to everyday situations has been seen in earlier stages, as it has involved sequencing events; describing, comparing and ordering the durations of events; reading the time on analog and digital clocks (including 24-hour time); converting between hours, minutes and seconds; using am and pm notation in real-life situations; and constructing timelines. |
In Stage 4, students learn the very important everyday-life skills of adding and subtracting time in mixed units (both mentally and by using a calculator) and solve related problems, as well as problems involving international time zones. The ability to compare times in, and calculate time differences between, major cities and areas of the world is of fundamental importance in international travel and also in everyday and work situations, such as communicating with people in other countries, watching overseas sporting events live on television, and conducting international business. |
| LANGUAGE | The words ‘minute’ (meaning ‘small’) and ‘minute’ (a time measure), although pronounced differently, are really the same word. A minute (time) is a minute (small) part of one hour. A minute (angle) is a minute (small) part of a right angle. |
EXPECTATIONS OF ATTAINMENT
| Solve problems involving duration, including using 12-hour and 24-hour time within a single time zone (ACMMG199) | add and subtract time mentally using bridging strategies, eg from 2:45 to 3:00 is 15 minutes and from 3:00 to 5:00 is 2 hours, so the time from 2:45 until 5:00 is 15 minutes + 2 hours = 2 hours 15 minutes, interpret and use timetables from real-life situations, including those involving 24-hour time {Literacy, Personal and social capability} |
| add and subtract time with a calculator, including by using the ‘degrees, minutes, seconds’ button | |
| round answers to time calculations to the nearest minute or hour | |
| interpret calculator displays for time calculations, eg 2.25 on a calculator display for a time calculation means 214 hours or 2 hours 15 minutes | |
| solve a variety of problems involving duration, including where times are expressed in 12-hour and 24-hour notation, that require the use of mixed units (years, months, days, hours and/or minutes) |
| Solve problems involving international time zones | compare times in, and calculate time differences between, major cities of the world, eg ‘Given that London is 10 hours behind Sydney, what time is it in London when it is 6:00 pm in Sydney?’Critical and creative thinking interpret and use information related to international time zones from maps (Problem Solving)Critical and creative thinking solve problems involving international time as it relates to everyday life, eg determine whether a particular soccer game can be watched live on television during normal waking hours (Problem Solving) |
PROPERTIES OF GEOMETRIC FIGURES
OUTCOME
A student:
MA4-17MG:
- classifies, describes and uses the properties of triangles and quadrilaterals, and determines congruent triangles to find unknown side lengths and angles
TEACHING POINTS | In Stage 4, the treatment of triangles and quadrilaterals is still informal, with students consolidating their understanding of different triangles and quadrilaterals and being able to identify them from their properties. Students who recognise class inclusivity and minimum requirements for definitions may address this Stage 4 content concurrently with content in Stage 5 Properties of Geometrical Figures, where properties of triangles and quadrilaterals are deduced from formal definitions. |
| Students who recognise class inclusivity and minimum requirements for definitions may address this Stage 4 content concurrently with content in Stage 5 Properties of Geometrical Figures, where properties of triangles and quadrilaterals are deduced from formal definitions. | |
| Students should give reasons orally and in written form for their findings and answers. For some students, formal setting out could be introduced. | |
| A range of examples of the various triangles and quadrilaterals should be given, including quadrilaterals containing a reflex angle and figures presented in different orientations. |
| LANGUAGE | In Stage 4, students should use full sentences to describe the properties of plane shapes, eg ‘The diagonals of a parallelogram bisect each other’. Students may not realise that in this context, the word ‘the’ implies ‘all’ and so this should be made explicit. Using the full name of the quadrilateral when describing its properties should assist students in remembering the geometrical properties of each particular shape. Students in Stage 4 should write geometrical reasons without the use of abbreviations to assist them in learning new terminology, and in understanding and retaining geometrical concepts. This syllabus uses the phrase ‘line(s) of symmetry’, although ‘axis/axes of symmetry’ may also be used. ‘Scalene’ is derived from the Greek word skalenos, meaning ‘uneven’. ‘Isosceles’ is derived from the Greek words isos, meaning ‘equals’, and skelos, meaning ‘leg’. ‘Equilateral’ is derived from the Latin words aequus, meaning ‘equal’, and latus, meaning ‘side’. ‘Equiangular’ is derived from aequus and another Latin word, angulus, meaning ‘corner’. |
EXPECTATIONS OF ATTAINMENT
| Classify triangles according to their side and angle properties and describe quadrilaterals | label and name triangles (eg triangle ABC or ΔABC) and quadrilaterals (eg ABCD) in text and on diagrams |
| use the common conventions to mark equal intervals on diagrams | |
recognise and classify types of triangles on the basis of their properties (acute-angled triangles, right-angled triangles, obtuse-angled triangles, equilateral triangles, isosceles triangles and scalene triangles)Literacy Critical and creative thinking
| |
| distinguish between convex and non-convex quadrilaterals (the diagonals of a convex quadrilateral lie inside the figure) | |
investigate the properties of special quadrilaterals (parallelograms, rectangles, rhombuses, squares, trapeziums and kites), including whether:
| |
classify special quadrilaterals on the basis of their propertiesLiteracy Critical and creative thinking
|
Identify line and rotational symmetries (ACMMG181) | investigate and determine lines (axes) of symmetry and the order of rotational symmetry of polygons, including the special quadrilateralsCritical and creative thinking Literacy
|
| investigate the line and rotational symmetries of circles and of diagrams involving circles, such as a sector or a circle with a marked chord or tangent | |
| identify line and rotational symmetries in pictures and diagrams, eg artistic and cultural designs |
Demonstrate that the angle sum of a triangle is 180° and use this to find the angle sum of a quadrilateral (ACMMG166) | justify informally that the interior angle sum of a triangle is 180°, and that any exterior angle equals the sum of the two interior opposite anglesLiteracy Critical and creative thinking
|
| use the angle sum of a triangle to establish that the angle sum of a quadrilateral is 360° | |
| use the angle sum results for triangles and quadrilaterals to determine unknown angles in triangles and quadrilaterals, giving reasons |
Use the properties of special triangles and quadrilaterals to solve simple numerical problems with appropriate reasoning | find unknown sides and angles embedded in diagrams, using the properties of special triangles and quadrilaterals, giving reasonsCritical and creative thinking
|
RIGHT ANGLED TRIANGLES (PYTHAGORAS)
OUTCOME
A student:
MA4-16MG:
- applies Pythagoras’ theorem to calculate side lengths in right-angled triangles, and solves related problems
| TEACHING POINTS | In Stage 3, students are continuing to develop their skills of visual imagery, including the ability to perceive and hold an appropriate mental image of an object or arrangement, and to predict the orientation or shape of an object that has been moved or altered. Also see Year 5 |
| LANGUAGE | Students should be able to communicate using the following language: object, shape, three-dimensional object (3D object), prism, cube, pyramid, base, uniform cross-section, face, edge, vertex (vertices), top view, front view, side view, net. |
EXPECTATIONS OF ATTAINMENT
| Investigate pythagoras-theorem and its application to solving simple problems involving right-angled triangles (ACMMG222) | identify the hypotenuse as the longest side in any right-angled triangle and also as the side opposite the right angle |
establish the relationship between the lengths of the sides of a right-angled triangle in practical ways, including with the use of digital technologiesInformation and communication technology capability Critical and creative thinking
| |
use Pythagoras’ theorem to find the length of an unknown side in a right-angled triangle
| |
| write answers to a specified or sensible level of accuracy, using an ‘approximately equals’ sign, ie ≑ or ≈ | |
solve a variety of practical problems involving Pythagoras’ theorem, approximating the answer as a decimal
| |
| identify a Pythagorean triad as a set of three numbers such that the sum of the squares of the first two equals the square of the third | |
| use the converse of Pythagoras’ theorem to establish whether a triangle has a right angle |
| Investigate the concept of irrational numbers (ACMNA186) | use technology to explore decimal approximations of surds
|
| solve a variety of practical problems involving Pythagoras’ theorem, giving exact answers (ie as surds where appropriate), eg √5 |
ANGLE RELATIONSHIPS
OUTCOME
A student:
MA4-18MG:
identifies and uses angle relationships, including those related to transversals on sets of parallel lines
| TEACHING POINTS | Students could explore the results relating to angles associated with parallel lines cut by a transversal by starting with corresponding angles and moving one vertex and all four angles to the other vertex by a translation. The other two results then follow, using vertically opposite angles and angles on a straight line. Alternatively, the equality of the alternate angles can be seen by rotation about the midpoint of the transversal. Students should give reasons when finding the sizes of unknown angles. For some students, formal setting out could be introduced. For example, ∠ABQ=70∘ (corresponding angles, AC∥PR). In his calculation of the circumference of the Earth, the Greek mathematician, geographer and astronomer Eratosthenes (c276–c194 BC) used parallel line results. |
| LANGUAGE | Students in Stage 4 should write geometrical reasons without the use of abbreviations to assist them in learning new terminology, and in understanding and retaining geometrical concepts, eg ‘When a transversal cuts parallel lines, the co-interior angles formed are supplementary’. Some students may find the use of the terms ‘complementary’ and ‘supplementary’ (adjectives) and ‘complement’ and ‘supplement’ (nouns) difficult. Teachers should model the use of these terms in sentences, both verbally and in written form, eg, ’50° and 40° are complementary angles’, ‘The complement of 50° is 40°’.
Students should be aware that complementary and supplementary angles may or may not be adjacent. |
| PURPOSE RELEVANCE OF SUBSTRAND | The development of knowledge and understanding of angle relationships, including the associated terminology, notation and conventions, is of fundamental importance in developing an appropriate level of knowledge, skills and understanding in geometry. Angle relationships and their application play an integral role in students learning to analyse geometry problems and developing geometric and deductive reasoning skills, as well as problem-solving skills. Angle relationships are key to the geometry that is important in the work of architects, engineers, designers, builders, physicists, land surveyors, etc, as well as the geometry that is common and important in everyday situations, such as in nature, sports, buildings, astronomy, art, etc. |
Expectations of Attainment
| Use the language, notation and conventions of geometry | define, label and name points, lines and intervals using capital letters |
| label the vertex and arms of an angle with capital letters | |
| label and name angles using ∠P or ∠QPR notation | |
| use the common conventions to indicate right angles and equal angles on diagrams |
| Recognise the geometrical properties of angles at a point | use the terms ‘complementary’ and ‘supplementary’ for angles adding to 90° and 180°, respectively, and the associated terms ‘complement’ and ‘supplement’ |
| use the term ‘adjacent angles’ to describe a pair of angles with a common arm and a common vertex, and lie on opposite sides of the common arm | |
identify and name right angles, straight angles, angles of complete revolution and vertically opposite angles embedded in diagramsLiteracy Critical and creative thinking
|
| Identify corresponding, alternate and co-interior angles when two straight lines are crossed by a transversal (ACMMG163) | identify and name perpendicular lines using the symbol for ‘is perpendicular to’ (⊥), eg AB⊥CD |
| use the common conventions to indicate parallel lines on diagrams | |
| identify and name pairs of parallel lines using the symbol for ‘is parallel to’ (∥), eg PQ∥RS | |
| define and identify ‘transversals’, including transversals of parallel lines | |
identify, name and measure alternate angle pairs, corresponding angle pairs and co-interior angle pairs for two lines cut by a transversalCritical and creative thinking
| |
| recognise the equal and supplementary angles formed when a pair of parallel lines is cut by a transversal |
| Investigate conditions for two lines to be parallel (ACMMG164) | use angle properties to identify parallel lines Critical and creative thinking
|
| Solve simple numerical problems using reasoning (ACMMG164) | find the sizes of unknown angles embedded in diagrams using angle relationships, including angles at a point and angles associated with parallel lines, giving reasons
|
STATISTICS AND PROBABILITY
DATA COLLECTION AND REPRESENTATION
OUTCOME
A student:
MA4-19SP:
collects, represents and interprets single sets of data, using appropriate statistical displays
| TEACHING POINTS | Students in Stage 4 can be expected to have some prior knowledge of both dot plots and line graphs, as these types of graph are introduced in Stage 3. They construct, describe and interpret column graphs in Stage 2 and Stage 3; however, histograms, divided bar graphs and sector graphs (pie charts) are not encountered until Stage 4. Statistical data is part of everyday life. Data may be displayed in tables or graphs, and may appear in all types of media. Graphs provide a visual overview of the substrand under investigation. Students should be aware that while many graphs are accurate and informative, some can be misleading. They need to experience interpreting a wide variety of graphical representations, including column graphs, dot plots, stem-and-leaf plots, divided bar graphs, sector graphs and line graphs. Students should be able to select an appropriate graph to represent the collected data. |
| RELEVANCE | In investigations, it is important to develop knowledge and understanding of the ways in which relevant and sufficient data can be collected, as well as the associated implications and limitations. It is also important to develop knowledge and understanding of what constitute appropriate sources of data, both primary and secondary. Data and statistics are used in many aspects of our everyday and working lives. Data is collected to provide information on many topics of interest and to assist in making decisions regarding important issues (eg projects aimed at improving or developing products or services). Users at all levels need to have skills in the organisation and display of the collected data for its interpretation and analysis. This can be achieved in a wide variety of ways, including through the use of frequency distribution tables and simple data displays/graphs, such as frequency histograms and polygons, dot plots, stem-and-leaf plots, divided bar graphs, sector graphs and line graphs. |
| LANGUAGE | In everyday language, the term ‘pie chart’ is often used in reference to sector graphs. |
Expectations of Attainment
| Investigate techniques for collecting data, including census, sampling and observation (ACMSP284) | define ‘variable’ in the context of statistics as something measurable or observable that is expected to change over time or between individual observations |
recognise variables as categorical or numerical (either discrete or continuous)Literacy
| |
| recognise and explain the difference between a ‘population’ and a ‘sample’ selected from a population when collecting data | |
investigate and determine the differences between collecting data by observation, census and samplingLiteracy Critical and creative thinking
|
| Explore the practicalities and implications of obtaining data through sampling using a variety of investigative processes (ACMSP206) | collect data using a random process, eg numbers from a page in a phone book, or from a random number generator |
identify issues that may make it difficult to obtain representative data from either primary or secondary sourcesCritical and creative thinking Ethical understanding
| |
| investigate and question the selection of data used to support a particular viewpoint, eg the selective use of data in product advertising |
| Identify and investigate issues involving numerical data collected from primary and secondary sources (ACMSP169) | identify the difference between data collected from primary and secondary sources, eg data collected in the classroom compared with data drawn from a media source |
explore issues involved in constructing and conducting surveys, such as sample size, bias, type of data required, and ethicsLiteracy Ethical understanding Civics and citizenship Difference and diversity
| |
construct appropriate survey questions and a related recording sheet in order to collect both numerical and categorical data about a matter of interestLiteracy Critical and creative thinking Personal and social capability Difference and diversity
| |
collect and interpret information from secondary sources, presented as tables and/or graphs, about a matter of interest, eg sporting data, information about the relationship between wealth or education and the health of populations of different countriesLiteracy Intercultural understanding Ethical understanding Civics and citizenship Difference and diversity
| |
use spreadsheets or statistical software packages to tabulate and graph dataInformation and communication technology capability
|
Construct and compare a range of data displays, including stem-and-leaf plots and dot plots (ACMSP170) | use a tally to organise data into a frequency distribution table |
construct and interpret frequency histograms and polygons
| |
construct dot plots
| |
construct ordered stem-and-leaf plots, including stem-and-leaf plots with two-digit stems
| |
construct divided bar graphs, sector graphs and line graphs, with and without the use of digital technologiesLiteracy
| |
interpret a variety of graphs, including dot plots, stem-and-leaf plots, divided bar graphs, sector graphs and line graphsLiteracy
|
SINGLE VARIABLE DATA ANALYSIS
OUTCOME
A student:
MA4-20SP:
analyses single sets of data using measures of location, and range
| TEACHING POINTS | Many opportunities occur in this substrand for students to strengthen their skills in: collecting, analysing and organising information; communicating ideas and information; planning and organising activities; working with others and in teams; using mathematical ideas and techniques; using technology, including spreadsheets. |
| RELEVANCE | Single-variable (or ‘univariate’) data analysis involves the statistical examination of a particular ‘variable’ (ie a value or characteristic that changes for different individuals, etc) and is of fundamental importance in the statistics used widely in everyday situations and in fields including education, business, economics and government. Most single-variable data analysis methods are used for descriptive purposes. In organising and displaying the data collected, frequencies, tables and a variety of data displays/graphs are used. These data displays/graphs, and numerical summary measures, are used to analyse and describe a data set in relation to a single variable, such as the scores on a test, and to compare a data set to other data sets. Single-variable data analysis is commonly used in the first stages of investigations, research, etc to describe and compare data sets, before being supplemented by more advanced ‘bivariate’ or ‘multivariate’ data analysis. |
| LANGUAGE | The term ‘average’, when used in everyday language, generally refers to the mean and describes a ‘typical value’ within a set of data. Students need to be provided with opportunities to discuss what information can be drawn from the data presented. They need to think about the meaning of the information and to put it into their own words. Language to be developed would include superlatives, comparatives, expressions such as ‘prefer … over’, etc. |
Expectations of Attainment
| Calculate mean, median, mode and range for sets of data and interpret these statistics in the context of data (ACMSP171) |
|
determine the median, mode and range for sets of data
| |
| identify and describe the mean, median and mode as ‘measures of location’ or ‘measures of centre’, and the range as a ‘measure of spread’ | |
describe, in practical terms, the meaning of the mean, median, mode and/or range in the context of the data, eg when referring to the mode of shoe-size data: ‘The most popular shoe size is size 7’ |
| Investigate the effect of individual data values, including outliers, on the mean and median (ACMSP207) | identify any clusters, gaps and outliers in sets of data |
investigate the effect of outliers on the mean, median, mode and range by considering a small set of data and calculating each measure, with and without the inclusion of an outlierCritical and creative thinking
| |
| analyse collected data to identify any obvious errors and justify the inclusion of any individual data values that differ markedly from the rest of the data collected |
| Describe and interpret data displays using mean, median and range (ACMSP172) | calculate measures of location (mean, median and mode) and the range for data represented in a variety of statistical displays, including frequency-distribution tables, frequency histograms, stem-and-leaf plots and dot plots |
| draw conclusions based on the analysis of data displays using the mean, median and/or mode, and range |
| Explore the variation of means and proportions of random samples drawn from the same population(ACMSP293) | investigate ways in which different random samples may be drawn from the same population, eg random samples from a census may be chosen by gender, postcode, state, etc |
| calculate and compare summary statistics (mean, median, mode and range) of at least three different random samples drawn from the same population use a spreadsheet to calculate and compare summary statistics of different random samples drawn from the same population (Communicating, Problem Solving)
|
Construct and compare a range of data displays, including stem-and-leaf plots and dot plots (ACMSP170) | use a tally to organise data into a frequency distribution table |
construct and interpret frequency histograms and polygons
| |
construct dot plots
| |
construct ordered stem-and-leaf plots, including stem-and-leaf plots with two-digit stems
| |
construct divided bar graphs, sector graphs and line graphs, with and without the use of digital technologiesLiteracy
| |
interpret a variety of graphs, including dot plots, stem-and-leaf plots, divided bar graphs, sector graphs and line graphsLiteracy
|
PROBABILITY 1
OUTCOME
A student:
MA4-21SP:
represents probabilities of simple and compound events
TEACHING POINTS | Probability is concerned with the level of certainty that a particular event will occur. The higher the probability of an event, the ‘more certain’ or ‘more likely’ it is that the event will occur. |
| Probability is used widely by governments and in many fields, including mathematics, statistics, science, business and economics. | |
| In everyday situations, probabilities are key to such areas as risk assessment, finance, and the reliability of products such as cars and electronic goods. It is therefore important across society that probabilities are understood and used appropriately in decision making. |
LANGUAGE | A simple event has outcomes that are equally likely. In a chance experiment, such as rolling a standard six-sided die once, an event might be one of the outcomes or a collection of the outcomes. For example, an event might be that an odd number is rolled, with the favourable outcomes being a ‘1’, a ‘3’ and a ‘5’. |
| It is important that students learn the correct terminology associated with probability. |
EXPECTATIONS OF ATTAINMENT
| Construct sample spaces for single-step experiments with equally likely outcomes (ACMSP167) | use the term ‘chance experiment’ when referring to actions such as tossing a coin, rolling a die, or randomly selecting an object from a bag |
| use the term ‘outcome’ to describe a possible result of a chance experiment and list all of the possible outcomes for a single-step experiment | |
| use the term ‘sample space’ to describe a list of all of the possible outcomes for a chance experiment, eg if a standard six-sided die is rolled once, the sample space is {1,2,3,4,5,6} | |
distinguish between equally likely outcomes and outcomes that are not equally likely in single-step chance experimentsLiteracy
|
| Assign probabilities to the outcomes of events and determine probabilities for events (ACMSP168) | use the term ‘event’ to describe either one outcome or a collection of outcomes in the sample space of a chance experiment, eg in the experiment of rolling a standard six-sided die once, obtaining the number ‘1’ is an ‘event’ and obtaining a number divisible by three is also an eventLiteracy
|
assign a probability of 0 to events that are impossible and a probability of 1 to events that are certain to occurLiteracy
| |
| assign probabilities to simple events by reasoning about equally likely outcomes, eg the probability of randomly drawing a card of the diamond suit from a standard pack of 52 playing cards is 13/52 = 1/4 | |
express the probability of an event, given a finite number of equally likely outcomes in the sample space, as
| |
solve probability problems involving single-step experiments using cards, dice, spinners, etc |
| Identify complementary events and use the sum of probabilities to solve problems (ACMSP204) | establish that the sum of the probabilities of all of the possible outcomes of a single-step experiment is 1 |
| identify and describe the complement of an event, eg the complement of the event ‘rolling a 6’ when rolling a die is ‘not rolling a 6’ | |
| establish that the sum of the probability of an event and its complement is 1, ie P (event) + P (complement of event) = 1 | |
| calculate the probability of a complementary event using the fact that the sum of the probabilities of complementary events is 1, eg the probability of ‘rolling a 6’ when rolling a die is 1/6, therefore the probability of the complementary event, ‘not rolling a 6’, is 1 – 1/6 = 5/6 |



