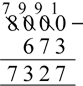YEAR 5 MATHS FOCUS
NUMBERS AND ALGEBRA
WHOLE NUMBERS
OUTCOME
A student:
MA3-4NA:
orders, reads and represents integers of any size and describes properties of whole numbers
TEACHING POINTS | In some Asian languages, such as Chinese, Japanese and Korean, the natural language structures used when expressing numbers larger than 10 000 are ‘tens of thousands’ rather than ‘thousands’, and ‘tens of millions’ rather than ‘millions’. For example, in Chinese (Mandarin), 612 000 is expressed as ’61 wàn, 2 qiān’, which translates as ’61 tens of thousands and 2 thousands’. |
The abbreviation ‘K’ is derived from the Greek word khilios, meaning ‘thousand’. It is used in many job advertisements to represent salaries (eg a salary of $70 K or $70 000). It is also used as an abbreviation for the size of computer files (eg a size of 20 K, meaning twenty thousand bytes). |
| LANGUAGE | Students should be able to communicate using the following language: ascending order, descending order, zero, ones, tens, hundreds, thousands, tens of thousands, hundreds of thousands, millions, digit, place value, expanded notation, round to, whole number, factor, highest common factor (HCF), multiple, lowest common multiple (LCM). |
Expectations of Attainment
Recognise, represent and order numbers to at least tens of millions | apply an understanding of place value and the role of zero to read and write numbers of any size {Literacy} |
| state the place value of digits in numbers of any size | |
| arrange numbers of any size in ascending and descending order | |
| record numbers of any size using expanded notation, eg 163 480 = 100 000 + 60 000 + 3000 + 400 + 80 | |
| partition numbers of any size in non-standard forms to aid mental calculation, eg when adding 163 480 and 150 000, 163 480 could be partitioned as 150 000 + 13 480, so that 150 000 could then be doubled and added to 13 480 {Critical and creative thinking} | |
| use numbers of any size in real-life situations, including in money problems | |
| – interpret information from the internet, the media, the environment and other sources that use large numbers {Communicating, Reasoning, Literacy, Information and communication technology capability, Personal and social capability, Work and enterprise} | |
| recognise different abbreviations of numbers used in everyday contexts, eg $350 K represents $350 000 {Literacy, Work and enterprise} | |
| round numbers to a specified place value, eg round 5 461 883 to the nearest million |
Identify and describe factors and multiples of whole numbers and use them to solve problems(ACMNA098) | determine all ‘factors’ of a given whole number, eg 36 has factors 1, 2, 3, 4, 6, 9, 12, 18 and 36 {Literacy} |
| determine the ‘highest common factor’ (HCF) of two whole numbers, eg the HCF of 16 and 24 is 8 {Literacy} | |
| determine ‘multiples’ of a given whole number, eg multiples of 7 are 7, 14, 21, 28, … {Literacy} | |
| determine the ‘lowest common multiple’ (LCM) of two whole numbers, eg the LCM of 21 and 63 is 63 {Literacy} | |
| determine whether a particular number is a factor of a given number using digital technologies {Critical and creative thinking} | |
| – recognise that when a given number is divided by one of its factors, the result must be a whole number {Problem Solving, Critical and creative thinking} | |
| solve problems using knowledge of factors and multiples, eg ‘There are 48 people at a party. In how many ways can you set up the tables and chairs, so that each table seats the same number of people and there are no empty chairs?’ {Critical and creative thinking} |
ADDITION & SUBTRACTION
OUTCOME
A student:
MA3-5NA:
selects and applies appropriate strategies for addition and subtraction with counting numbers of any size
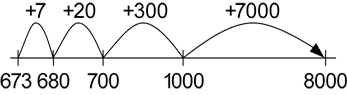
STRATEGIES | Written strategies using informal mental strategies (empty number line):
The difference can be shifted one unit to the left on an empty number line, so that 8000 − 673 becomes 7999 − 672, which is an easier subtraction to calculate.
|
Written strategies using a formal algorithm (decomposition method):
|
TEACHING POINTS | In Stage 3, mental strategies need to be continually reinforced.
|
| Students may find recording (writing out) informal mental strategies to be more efficient than using formal written algorithms, particularly in the case of subtraction. |
LANGUAGE | Students should be able to communicate using the following language: plus, sum, add, addition, increase, minus, the difference between, subtract, subtraction, decrease, equals, is equal to, empty number line, strategy, digit, estimate, round to, budget. |
| Teachers should model and use a variety of expressions for the operations of addition and subtraction, and should draw students’ attention to the fact that the words used for subtraction may require the operation to be performed with the numbers in the reverse order to that in which they are stated in the question. For example, ‘9 take away 3’ and ‘reduce 9 by 3’ require the operation to be performed with the numbers in the same order as they are presented in the question (ie 9 – 3). However, ‘take 9 from 3’, ‘subtract 9 from 3’ and ‘9 less than 3’ require the operation to be performed with the numbers in the reverse order to that in which they are stated in the question (i.e. 3 – 9). |
Expectations of Attainment
Use efficient mental and written strategies and apply appropriate digital technologies to solve problems (ACMNA291) | use the term ‘sum’ to describe the result of adding two or more numbers, eg ‘The sum of 7 and 5 is 12’ {Literacy} |
| add three or more numbers with different numbers of digits, with and without the use of digital technologies, eg 42 000 + 5123 + 246 | |
| select and apply efficient mental, written and calculator strategies to solve addition and subtraction word problems, including problems involving money {Literacy, Information and communication technology capability, Critical and creative thinking} | |
| – interpret the words ‘increase’ and ‘decrease’ in addition and subtraction word problems, eg ‘If a computer costs $1599 and its price is then decreased by $250, how much do I pay?’ {Communicating, Problem Solving, Literacy} | |
| record the strategy used to solve addition and subtraction word problems | |
| – use empty number lines to record mental strategies {Communicating, Problem Solving} | |
| – use selected words to describe each step of the solution process {Communicating, Problem Solving, Literacy} | |
| check solutions to problems, including by using the inverse operation {Critical and creative thinking} |
Use estimation and rounding to check the reasonableness of answers to calculations (ACMNA099) | round numbers appropriately when obtaining estimates to numerical calculations |
| use estimation to check the reasonableness of answers to addition and subtraction calculations, e.g. 1438 + 129 is about 1440 + 130 {Critical and creative thinking} |
Create simple financial plans (ACMNA106) | use knowledge of addition and subtraction facts to create a financial plan, such as a budget, eg organise a class celebration on a budget of $60 for all expenses {Personal and social capability, Work and enterprise} |
| – record numerical data in a simple spreadsheet {Communicating, Information and communication technology capability} | |
| – give reasons for selecting, prioritising and deleting items when creating a budget {Communicating, Reasoning, Critical and creative thinking, Personal and social capability, Work and enterprise} |
MULTIPLICATION & DIVISION
OUTCOME
A student:
MA3-6NA:
selects and applies appropriate strategies for multiplication and division, and applies the order of operations to calculations involving more than one operation
TEACHING POINTS | Students could extend their recall of number facts beyond the multiplication facts to 10 × 10 by memorising multiples of numbers such as 11, 12, 15, 20 and 25. They could also utilise mental strategies, eg ’14 × 6 is 10 sixes plus 4 sixes’. |
| In Stage 3, mental strategies need to be continually reinforced. | |
| Students may find recording (writing out) informal mental strategies to be more efficient than using formal written algorithms, particularly in the case of multiplication. | |
| An inverse operation is an operation that reverses the effect of the original operation. Addition and subtraction are inverse operations; multiplication and division are inverse operations. | |
| The area model for two-digit by two-digit multiplication in Stage 3 is a precursor to the use of the area model for the expansion of binomial products in Stage 5. |
LANGUAGE | Students should be able to communicate using the following language: multiply, multiplied by, product, multiplication, multiplication facts, area, thousands, hundreds, tens, ones, double, multiple, factor, divide, divided by, quotient, division, halve, remainder, fraction, decimal, equals, strategy, digit, estimate, round to. |
| In mathematics, ‘quotient’ refers to the result of dividing one number by another. | |
| Teachers should model and use a variety of expressions for multiplication and division. They should draw students’ attention to the fact that the words used for division may require the operation to be performed with the numbers in the reverse order to that in which they are stated in the question. For example, ‘divide 6 by 2’ and ‘6 divided by 2’ require the operation to be performed with the numbers in the same order as they are presented in the question (ie 6 ÷ 2). However, ‘How many 2s in 6?’ requires the operation to be performed with the numbers in the reverse order to that in which they are stated in the question (ie 6 ÷ 2). | |
| The terms ‘ratio’ and ‘rate’ are not introduced until Stage 4, but students need to be able to interpret problems involving simple rates as requiring multiplication or division. |
Expectations of Attainment
Solve problems involving multiplication of large numbers by one- or two-digit numbers using efficient mental and written strategies and appropriate digital technologies (ACMNA100) | use mental and written strategies to multiply three- and four-digit numbers by one-digit numbers, including: {Critical and creative thinking} – multiplying the thousands, then the hundreds, then the tens and then the ones, eg 673×4=(600×4)+(70×4)+(3×4)=2400+280+12=2692 – using an area model, e.g. 684 × 5 – using the formal algorithm, e.g. 432 × 5 |
| use mental and written strategies to multiply two- and three-digit numbers by two-digit numbers, including: {Critical and creative thinking} – using an area model for two-digit by two-digit multiplication, e.g. 25 × 26 – factorising the numbers, e.g. 12 × 25 = 3 × 4 × 25 = 3 × 100 = 300 – using the extended form (long multiplication) of the formal algorithm, e.g. | |
| use digital technologies to multiply numbers of up to four digits {Information and communication technology capability} | |
| – check answers to mental calculations using digital technologies {Problem Solving, Information and communication technology capability} | |
| apply appropriate mental and written strategies, and digital technologies, to solve multiplication word problems {Literacy, Information and communication technology capability, Critical and creative thinking} | |
| – use the appropriate operation when solving problems in real-life situations {Problem Solving} | |
| – use inverse operations to justify solutions {Problem Solving, Reasoning, Critical and creative thinking} | |
| record the strategy used to solve multiplication word problems {Literacy} | |
| – use selected words to describe each step of the solution process {Communicating, Problem Solving, Literacy} |
Solve problems involving division by a one-digit number, including those that result in a remainder (ACMNA101) | use the term ‘quotient’ to describe the result of a division calculation, e.g. ‘The quotient when 30 is divided by 6 is 5’ |
| recognise and use different notations to indicate division, e.g. 25÷4, 4)25, 25/4 {Literacy} | |
| record remainders as fractions and decimals, eg 25÷4=6 1/4 or 6.25 {Literacy} | |
| use mental and written strategies to divide a number with three or more digits by a one-digit divisor where there is no remainder, including: {Critical and creative thinking} – dividing the hundreds, then the tens, and then the ones, e.g. 3248 ÷ 4 3200÷4=800 40÷4=10 8÷4=2 so 3248÷4=812 – using the formal algorithm, eg 258 ÷ 6 43 6)258 | |
| use mental and written strategies to divide a number with three or more digits by a one-digit divisor where there is a remainder, including: {Critical and creative thinking} – dividing the tens and then the ones, e.g. 243 ÷ 4 240÷4=60 3÷4=3/4 so 243÷4=60 3/4 – using the formal algorithm, e.g. 587 ÷ 6 97 5/6 6)258 | |
| – explain why the remainder in a division calculation is always less than the number divided by (the divisor) {Communicating, Reasoning, Critical and creative thinking} | |
| show the connection between division and multiplication, including where there is a remainder, e.g. 25 ÷ 4 = 6 remainder 1, so 25 = 4 × 6 + 1 | |
| use digital technologies to divide whole numbers by one- and two-digit divisors {Information and communication technology capability} | |
| – check answers to mental calculations using digital technologies {Problem Solving, Information and communication technology capability} | |
| apply appropriate mental and written strategies, and digital technologies, to solve division word problems {Literacy, Information and communication technology capability, Critical and creative thinking} | |
| – recognise when division is required to solve word problems {Problem Solving} | |
| – use inverse operations to justify solutions to problems {Problem Solving, Reasoning, Critical and creative thinking} | |
| use and interpret remainders in solutions to division problems, eg recognise when it is appropriate to round up an answer, such as ‘How many 5-seater cars are required to take 47 people to the beach?’ {Critical and creative thinking} | |
| record the strategy used to solve division word problems {Literacy} | |
| – use selected words to describe each step of the solution process {Communicating, Problem Solving, Literacy} |
Use estimation and rounding to check the reasonableness of answers to calculations (ACMNA099) | round numbers appropriately when obtaining estimates to numerical calculations |
| use estimation to check the reasonableness of answers to multiplication and division calculations, e.g. ’32 × 253 will be about, but more than, 30 × 250′ |
FRACTIONS & DECIMALS
OUTCOME
A student:
MA3-7NA:
compares, orders and calculates with fractions, decimals and percentages
TEACHING POINTS | In Stage 3 Fractions and Decimals, students study fractions with denominators of 2, 3, 4, 5, 6, 8, 10, 12 and 100. A unit fraction is any proper fraction in which the numerator is 1, eg 12, 13, 14, 15, … |
| Students need to interpret a variety of word problems and translate them into mathematical diagrams and/or fraction notation. Fractions have different meanings depending on the context, eg show on a diagram three-quarters (3/4) of a pizza, draw a diagram to show how much each child receives when four children share three pizzas. | |
Fractions may be interpreted in different ways depending on the context, eg two-quarters (2/4) may be thought of as two equal parts of one whole that has been divided into four equal parts. The image shows 1 square divided into quarters. Two-quarters are shaded.
| |
Alternatively, two-quarters (2/4) may be thought of as two equal parts of two wholes that have each been divided into quarters. 2 squares, each divided into quarters, 2 of which are shaded: ‘one-quarter + one-quarter = two-quarters’. 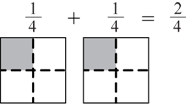 |
LANGUAGE | Students should be able to communicate using the following language: whole, equal parts, half, quarter, eighth, third, sixth, twelfth, fifth, tenth, hundredth, thousandth, one-thousandth, fraction, numerator, denominator, mixed numeral, whole number, number line, proper fraction, improper fraction, decimal, decimal point, digit, place value, decimal places. |
| The decimal 1.12 is read as ‘one point one two’ and not ‘one point twelve’. | |
| When expressing fractions in English, the numerator is said first, followed by the denominator. However, in many Asian languages (e.g. Chinese, Japanese), the opposite is the case: the denominator is said before the numerator. |
Expectations of Attainment
Compare and order common unit fractions and locate and represent them on a number line (ACMNA102) | place fractions with denominators of 2, 3, 4, 5, 6, 8, 10 and 12 on a number line between 0 and 1, e.g. 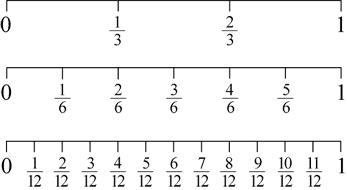 |
| compare and order unit fractions with denominators of 2, 3, 4, 5, 6, 8, 10, 12 and 100 {Critical and creative thinking} | |
| – compare the relative value of unit fractions by placing them on a number line between 0 and 1 {Communicating, Reasoning} | |
| – investigate and explain the relationship between the value of a unit fraction and its denominator {Communicating, Reasoning, Critical and creative thinking} |
Investigate strategies to solve problems involving addition and subtraction of fractions with the same denominator (ACMNA103) | identify and describe ‘proper fractions’ as fractions in which the numerator is less than the denominator {Literacy} |
| identify and describe ‘improper fractions’ as fractions in which the numerator is greater than the denominator {Literacy} | |
express mixed numerals as improper fractions and vice versa, through the use of diagrams and number lines, leading to a mental strategy, e.g. {Literacy} | |
model and represent strategies, including using diagrams, to add proper fractions with the same denominator, where the result may be a mixed numeral, e.g.  | |
| model and represent a whole number added to a proper fraction, e.g. 2+3/4=2 3/4 | |
| subtract a proper fraction from another proper fraction with the same denominator, e.g. 7/8−2/8=5/8 | |
model and represent strategies, including using diagrams, to add mixed numerals with the same denominator, e.g.
| |
use diagrams, and mental and written strategies, to subtract a unit fraction from any whole number including 1, e.g. | |
| solve word problems that involve addition and subtraction of fractions with the same denominator, eg ‘I eat 1/5 of a block of chocolate and you eat 3/5 of the same block. How much of the block of chocolate has been eaten?’ {Critical and creative thinking} | |
| – use estimation to verify that an answer is reasonable {Problem Solving, Reasoning, Critical and creative thinking} |
Recognise that the place value system can be extended beyond hundredths (ACMNA104) | express thousandths as decimals |
| interpret decimal notation for thousandths, e.g. 0.123=123/1000 | |
| state the place value of digits in decimal numbers of up to three decimal places |
Compare, order and represent decimals (ACMNA105) | compare and order decimal numbers of up to three decimal places, eg 0.5, 0.125, 0.25 {Literacy} |
| interpret zero digit(s) at the end of a decimal, eg 0.170 has the same value as 0.17 | |
| place decimal numbers of up to three decimal places on a number line between 0 and 1 |
PATTERNS & ALGEBRA
OUTCOME
A student:
MA3-8NA:
analyses and creates geometric and number patterns, constructs and completes number sentences, and locates points on the Cartesian plane
TEACHING POINTS | In Stage 3, students should be encouraged to use their own words to describe number patterns. Patterns can usually be described in more than one way and it is important for students to hear how other students describe the same pattern. Students’ descriptions of number patterns can then become more sophisticated as they experience a variety of ways of describing the same pattern. The teacher could begin to model the use of more appropriate mathematical language to encourage this development… |
| This substrand involves algebra without using letters to represent unknown values. When calculating unknown values, students need to be encouraged to work backwards and to describe the processes using inverse operations, rather than using trial-and-error methods. The inclusion of number sentences that do not have whole-number solutions will aid this process. | |
| To represent equality of mathematical expressions, the terms ‘is the same as’ and ‘is equal to’ should be used. Use of the word ‘equals’ may suggest that the right-hand side of an equation contains ‘the answer’, rather than a value equivalent to that on the left. |
| LANGUAGE | Students should be able to communicate using the following language: pattern, increase, decrease, missing number, number sentence, number line. |
Expectations of Attainment
Describe, continue and create patterns with fractions, decimals and whole numbers resulting from addition and subtraction (ACMNA107) | identify, continue and create simple number patterns involving addition and subtraction {Critical and creative thinking} |
| describe patterns using the terms ‘increase’ and ‘decrease’, eg for the pattern 48, 41, 34, 27, …, ‘The terms decrease by seven’ {Literacy} | |
| create, with materials or digital technologies, a variety of patterns using whole numbers, fractions or decimals, e.g. 1/4, 2/4, 3/4, 4/4, 5/4, 6/4, … or 2.2, 2.0, 1.8, 1.6, … {Information and communication technology capability, Critical and creative thinking} | |
| use a number line or other diagram to create patterns involving fractions or decimals |
Use equivalent number sentences involving multiplication and division to find unknown quantities (ACMNA121) | complete number sentences that involve more than one operation by calculating missing numbers, e.g. 5×□=4×10, 5×□=30−10 |
| – describe strategies for completing simple number sentences and justify solutions {Communicating, Reasoning, Critical and creative thinking} | |
| identify and use inverse operations to assist with the solution of number sentences, e.g. 125÷5=□ becomes □×5=125 | |
| – describe how inverse operations can be used to solve a number sentence {Communicating, Reasoning, Critical and creative thinking} | |
| complete number sentences involving multiplication and division, including those involving simple fractions or decimals, e.g. 7×□=7.7 | |
| – check solutions to number sentences by substituting the solution into the original question {Reasoning, Critical and creative thinking} | |
| write number sentences to match word problems that require finding a missing number, e.g. ‘I am thinking of a number that when I double it and add 5, the answer is 13. What is the number?’ {Literacy} |
MEASUREMENT AND GEOMETRY
LENGTH
OUTCOME
A student:
MA3-9MG:
selects and uses the appropriate unit and device to measure lengths and distances, calculates perimeters, and converts between units of length
TEACHING POINTS | When students are able to measure efficiently and effectively using formal units, they should be encouraged to apply their knowledge and skills in a variety of contexts. Following this, they should be encouraged to generalise their method for calculating the perimeters of squares, rectangles and triangles. |
When recording measurements, a space should be left between the number and the abbreviated unit, e.g. 3 cm, not 3cm. |
LANGUAGE | Students should be able to communicate using the following language: length, distance, kilometre, metre, centimetre, millimetre, measure, measuring device, ruler, tape measure, trundle wheel, estimate, perimeter, dimensions, width. |
Perimeter’ is derived from the Greek words that mean to measure around the outside: peri, meaning ‘around’, and metron, meaning ‘measure’. |
Expectations of Attainment
Choose appropriate units of measurement for length (ACMMG108) | recognise the need for a formal unit longer than the metre for measuring distance |
| recognise that there are 1000 metres in one kilometre, ie 1000 metres = 1 kilometre {Literacy} | |
| – describe one metre as one thousandth of a kilometre {Communicating, Literacy} | |
| measure a kilometre and a half-kilometre | |
| record distances using the abbreviation for kilometres (km) {Literacy} | |
| select and use the appropriate unit and measuring device to measure lengths and distances | |
| – describe how a length or distance was estimated and measured {Communicating, Problem Solving} | |
| – question and explain why two students may obtain different measures for the same length, distance or perimeter {Communicating, Reasoning, Critical and creative thinking} | |
| estimate lengths and distances using an appropriate unit and check by measuring | |
| record lengths and distances using combinations of millimetres, centimetres, metres and kilometres, e.g. 1 km 200 m |
Calculate the perimeters of rectangles using familiar metric units (ACMMG109) | use the term ‘dimensions’ to describe the ‘lengths’ and ‘widths’ of rectangles {Literacy} |
| measure and calculate the perimeter of a large rectangular section of the school, e.g. a playground, netball courts | |
| calculate perimeters of common two-dimensional shapes, including squares, rectangles, triangles and regular polygons with more than four sides (i.e. regular polygons other than equilateral triangles and squares) | |
| – recognise that rectangles with the same perimeter may have different dimensions {Reasoning, Critical and creative thinking} | |
| – explain that the perimeters of two-dimensional shapes can be found by finding the sum of the side lengths {Communicating} | |
| – explain the relationship between the lengths of the sides and the perimeters for regular polygons (including equilateral triangles and squares) {Communicating, Reasoning, Critical and creative thinking} | |
| record calculations used to find the perimeters of two-dimensional shapes |
AREA
OUTCOME
A student:
MA3-10MG:
selects and uses the appropriate unit to calculate areas, including areas of squares, rectangles and triangles
TEACHING POINTS | Students should have a clear understanding of the distinction between perimeter and area. |
| It is important in Stage 3 that students establish a real reference for the square kilometre and the hectare, eg locating an area of one square kilometre or an area of one hectare on a local map. | |
| When students are able to measure efficiently and effectively using formal units, they should be encouraged to apply their knowledge and skills in a variety of contexts. | |
| Students could be encouraged to find more efficient ways of counting when determining area, such as finding how many squares in one row and multiplying this by the number of rows. They should then begin to generalise their methods to calculate the areas of rectangles (including squares) and triangles. | |
| When generalising their methods to calculate areas, students in Stage 3 should use words. Algebraic formulas for areas are not introduced until Stage 4. |
LANGUAGE | Students should be able to communicate using the following language: area, measure, square centimetre, square metre, square kilometre, hectare, dimensions, length, width. |
| The abbreviation m^2 is read as ‘square metre(s)’ and not ‘metre(s) squared’ or ‘metre(s) square’. | |
| The abbreviation cm^2 is read as ‘square centimetre(s)’ and not ‘centimetre(s) squared’ or ‘centimetre(s) square’. |
EXPECTATIONS OF ATTAINMENT
Choose appropriate units of measurement for area (ACMMG108) | recognise the need for a formal unit larger than the square metre |
| identify situations where square kilometres are used for measuring area, eg a suburb {Critical and creative thinking} | |
| recognise and explain the need for a more convenient unit than the square kilometre | |
| recognise that there are 10 000 square metres in one hectare, ie 10 000 square metres = 1 hectare | |
| – equate one hectare to the area of a square with side lengths of 100 m {Communicating} | |
| – relate the hectare to common large pieces of land, including courts and fields for sports {Reasoning} | |
| – determine the dimensions of different rectangles with an area of one hectare {Problem Solving, Critical and creative thinking} | |
| record areas using the abbreviations for square kilometres (km2) and hectares (ha) {Literacy} |
Calculate the areas of rectangles using familiar metric units (ACMMG109) | establish the relationship between the lengths, widths and areas of rectangles (including squares) {Critical and creative thinking} |
| – explain that the area of a rectangle can be found by multiplying the length by the width {Communicating, Reasoning} | |
| record, using words, the method for finding the area of any rectangle, e.g. ‘Area of rectangle = length × width’ {Literacy} | |
| calculate areas of rectangles (including squares) in square centimetres and square metres | |
| – recognise that rectangles with the same area may have different dimensions {Reasoning, Critical and creative thinking} | |
| – connect factors of a number with the whole-number dimensions of different rectangles with the same area {Reasoning, Critical and creative thinking} | |
| record calculations used to find the areas of rectangles (including squares) | |
| apply measurement skills to solve problems involving the areas of rectangles (including squares) in everyday situations, e.g. determine the area of a basketball court | |
| measure the dimensions of a large rectangular piece of land in metres and calculate its area in hectares, e.g. the local park {Sustainability} |
VOLUME & CAPACITY
OUTCOME
A student:
MA3-11MG:
selects and uses the appropriate unit to estimate, measure and calculate volumes and capacities, and converts between units of capacity
TEACHING POINTS | The attribute of volume is the amount of space occupied by an object or substance and is usually measured in cubic units, eg cubic centimetres (cm^3) and cubic metres (m^3). |
| Capacity refers to the amount a container can hold and is measured in units, such as millilitres (mL), litres (L) and kilolitres (kL). Capacity is only used in relation to containers and generally refers to liquid measurement. The capacity of a closed container will be slightly less than its volume – capacity is based on the inside dimensions, while volume is determined by the outside dimensions of the container. It is not necessary to refer to these definitions with students (capacity is not taught as a concept separate from volume until Stage 4). | |
| Once students are able to measure efficiently and effectively using formal units, they could use centimetre cubes to construct rectangular prisms, counting the number of cubes to determine volume, and then begin to generalise their method for calculating the volume. | |
| The cubic metre can be related to the metre as a unit to measure length and the square metre as a unit to measure area. It is important that students are given opportunities to reflect on their understanding of length and area so that they can use this to calculate volume. |
LANGUAGE | Students should be able to communicate using the following language: capacity, container, volume, layers, cubic centimetre, cubic metre, measure, estimate. |
| The abbreviation m^3 is read as ‘cubic metre(s)’ and not ‘metre(s) cubed’. |
EXPECTATIONS OF ATTAINMENT
Choose appropriate units of measurement for volume and capacity (ACMMG108) | select and use appropriate units to measure the capacities of a variety of containers, e.g. millilitres for a drinking glass, litres for a water urn |
| measure the volumes of rectangular containers by packing them with cubic-centimetre blocks | |
| – explain the advantages and disadvantages of using cubic-centimetre blocks as a unit to measure volume {Communicating, Reasoning, Critical and creative thinking} | |
| – describe arrangements of cubic-centimetre blocks in containers in terms of layers, eg 5 layers of 8 cubic-centimetre blocks {Problem Solving} | |
| recognise the need for a formal unit larger than the cubic centimetre | |
| construct and use the cubic metre as a unit to measure larger volumes | |
| – explain why volume is measured in cubic metres in certain situations, e.g. wood bark, soil, concrete {Communicating, Reasoning, Critical and creative thinking} | |
| – recognise that a cubic metre can have dimensions other than a cube of side 1 metre, e.g. 2 metres by 1/2 metre by 1 metre {Problem Solving, Critical and creative thinking} | |
| record volumes using the abbreviation for cubic metres (m^3) {Literacy} | |
| estimate the size of a cubic metre, half a cubic metre and two cubic metres | |
| select and use appropriate units to estimate the volumes of a variety of objects, e.g. cubic centimetres for a lolly jar, cubic metres for the classroom |
MASS
OUTCOME
A student:
MA3-12MG:
selects and uses the appropriate unit and device to measure the masses of objects, and converts between units of mass
TEACHING POINTS | Gross mass is the mass of the contents of a container and the container. Net mass is the mass of the contents only. |
| Local industries and businesses could provide sources for the study of measurement in tonnes, eg weighbridges, cranes, hoists. |
LANGUAGE | Students should be able to communicate using the following language: mass, gross mass, net mass, measure, device, scales, tonne, kilogram, gram. |
| As the terms ‘weigh’ and ‘weight’ are common in everyday usage, they can be accepted in student language should they arise (although Gabi disagrees as it was frustrating having to unlearn this at university). Weight is a force that changes with gravity, while mass remains constant. |
EXPECTATIONS OF ATTAINMENT
Choose appropriate units of measurement for mass (ACMMG108) | recognise the need for a formal unit larger than the kilogram |
| use the tonne to record large masses, e.g. sand, soil, vehicles | |
| record masses using the abbreviation for tonnes (t) {Literacy} | |
| distinguish between the ‘gross mass’ and the ‘net mass’ of containers holding substances, e.g. cans of soup {Literacy} | |
| – interpret information about mass on commercial packaging {Communicating, Literacy} | |
| – solve problems involving gross mass and net mass, e.g. find the mass of a container given the gross mass and the net mass {Problem Solving, Critical and creative thinking} | |
| select and use the appropriate unit and device to measure mass, e.g. electronic scales, kitchen scales | |
| – determine the net mass of the contents of a container after measuring the gross mass and the mass of the container {Problem Solving, Critical and creative thinking} | |
| find the approximate mass of a small object by establishing the mass of a number of that object, eg ‘The stated weight of a box of chocolates is 250 g. If there are 20 identical chocolates in the box, what does each chocolate weigh?’ {Critical and creative thinking} |
TIME
OUTCOME
A student:
MA3-13MG:
uses 24-hour time and am and pm notation in real-life situations, and constructs timelines
TEACHING POINTS | Australia is divided into three time zones. In non-daylight saving periods, time in Queensland, New South Wales, Victoria and Tasmania is Eastern Standard Time (EST), time in South Australia and the Northern Territory is half an hour behind EST, and time in Western Australia is two hours behind EST. |
| Typically, 24-hour time is recorded without the use of the colon (:), e.g. 3:45 pm is written as 1545 or 1545 h and read as ‘fifteen forty-five hours’. |
| LANGUAGE | Students should be able to communicate using the following language: 12-hour time, 24-hour time, time zone, daylight saving, local time, hour, minute, second, am (notation), pm (notation) |
EXPECTATIONS OF ATTAINMENT
Compare 12- and 24-hour time systems and convert between them (ACMMG110) | tell the time accurately using 24-hour time, e.g. ‘2330 is the same as 11:30 pm’ {Literacy} |
| – describe circumstances in which 24-hour time is used, eg transport, armed forces, digital technologies {Communicating, Critical and creative thinking} | |
| convert between 24-hour time and time given using am or pm notation {Literacy} | |
| compare the local times in various time zones in Australia, including during daylight saving |
Determine and compare the duration of events | select an appropriate unit to measure a particular period of time |
| use a stopwatch to measure and compare the duration of events | |
| order a series of events according to the time taken to complete each one | |
| use start and finish times to calculate the elapsed time of events, eg the time taken to travel from home to school |
THREE-DIMENSIONAL SPACE
OUTCOME
A student:
MA3-14MG:
identifies three-dimensional objects, including prisms and pyramids, on the basis of their properties, and visualises, sketches and constructs them given drawings of different views
TEACHING POINTS | In Stage 3, the formal names for particular prisms and pyramids are introduced while students are engaged in their construction and representation. (Only ‘family’ names, such as prism, were introduced in Stage 2.) This syllabus names pyramids in the following format: square pyramid, pentagonal pyramid, etc. However, it is also acceptable to name pyramids using the word ‘based’, eg square-based pyramid, pentagonal-based pyramid. |
| Prisms have two bases that are the same shape and size. The bases of a prism may be squares, rectangles, triangles or other polygons. The other faces are rectangular if the faces are perpendicular to the bases. The base of a prism is the shape of the uniform cross-section, not necessarily the face on which it is resting. | |
| Pyramids differ from prisms as they have only one base and all the other faces are triangular. The triangular faces meet at a common vertex (the apex). Pyramids do not have a uniform cross-section. | |
| Spheres, cones and cylinders do not fit into the classification of prisms or pyramids as they have curved surfaces, not faces, eg a cylinder has two flat surfaces and one curved surface. | |
| A section is a representation of an object as it would appear if cut by a plane, eg if the corner were cut off a cube, the resulting cut face would be a triangle. An important understanding in Stage 3 is that the cross-sections parallel to the base of a prism are uniform and the cross-sections parallel to the base of a pyramid are not. | |
| Students could explore these ideas by stacking uniform objects to model prisms, and by stacking sets of seriated shapes to model pyramids. Note: such stacks are not strictly pyramids, but they do assist understanding. | |
| In geometry, a three-dimensional object is called a solid. The three-dimensional object may in fact be hollow, but it is still defined as a geometrical solid. |
LANGUAGE | Students should be able to communicate using the following language: object, shape, three-dimensional object (3D object), prism, cube, pyramid, base, uniform cross-section, face, edge, vertex (vertices), apex, top view, front view, side view, depth, net. |
| In Stage 1, students were introduced to the terms ‘flat surface’ and ‘curved surface’ for use in describing cones, cylinders and spheres, and the terms ‘faces’, ‘edges’ and ‘vertices’ for use in describing prisms and pyramids. |
EXPECTATIONS OF ATTAINMENT
Compare, describe and name prisms and pyramids | identify and determine the number of pairs of parallel faces of three-dimensional objects, e.g. ‘A rectangular prism has three pairs of parallel faces’ |
| identify the ‘base’ of prisms and pyramids {Literacy} | |
| – recognise that the base of a prism is not always the face where the prism touches the ground {Reasoning} | |
| name prisms and pyramids according to the shape of their base, e.g. rectangular prism, square pyramid {Literacy} | |
| visualise and draw the resulting cut face (plane section) when a three-dimensional object receives a straight cut {Critical and creative thinking} | |
| recognise that prisms have a ‘uniform cross-section’ when the section is parallel to the base | |
| – recognise that the base of a prism is identical to the uniform cross-section of the prism {Reasoning} | |
| – recognise a cube as a special type of prism {Communicating} | |
| recognise that pyramids do not have a uniform cross-section when the section is parallel to the base | |
| identify, describe and compare the properties of prisms and pyramids, including: {Literacy} number of faces shape of faces number and type of identical faces number of vertices number of edges | |
| – describe similarities and differences between prisms and pyramids, eg between a triangular prism and a hexagonal prism, between a rectangular prism and a rectangular(-based) pyramid {Communicating, Reasoning, Critical and creative thinking} | |
| – determine that the faces of prisms are always rectangles except the base faces, which may not be rectangles {Reasoning, Critical and creative thinking} | |
| – determine that the faces of pyramids are always triangles except the base face, which may not be a triangle {Reasoning, Critical and creative thinking} | |
| use the term ‘apex’ to describe the highest point above the base of a pyramid or cone {Literacy} |
Connect three-dimensional objects with their nets and other two-dimensional representations (ACMMG111) | visualise and sketch three-dimensional objects from different views, including top, front and side views {Critical and creative thinking} |
| – reflect on their own drawing of a three-dimensional object and consider how it can be improved {Reasoning, Critical and creative thinking, Personal and social capability} | |
| examine a diagram to determine whether it is or is not the net of a closed three-dimensional object {Critical and creative thinking} | |
| – explain why a given net will not form a closed three-dimensional object {Communicating, Reasoning} | |
| visualise and sketch nets for given three-dimensional objects {Critical and creative thinking} | |
| – recognise whether a diagram is a net of a particular three-dimensional object {Reasoning, Critical and creative thinking} | |
| visualise and name prisms and pyramids, given diagrams of their nets {Critical and creative thinking} | |
| – select the correct diagram of a net for a given prism or pyramid from a group of similar diagrams where the others are not valid nets of the object {Reasoning, Critical and creative thinking} | |
| show simple perspective in drawings by showing depth {Critical and creative thinking} |
TWO-DIMENSIONAL SPACE
OUTCOME
A student:
MA3-15MG:
manipulates, classifies and draws two-dimensional shapes, including equilateral, isosceles and scalene triangles, and describes their properties
TEACHING POINTS | A shape has rotational symmetry if a tracing of the shape, rotated part of a full turn around its centre, matches the original shape exactly. |
The order of rotational symmetry refers to the number of times a figure coincides with its original position in turning through one full rotation. If the order of rotational symmetry is 1, the shape does not have rotational symmetry. e.g.
| |
| Scalene’ is derived from the Greek word skalenos, meaning ‘uneven’; our English word ‘scale’ is derived from the same word. ‘Isosceles’ is derived from the Greek words isos, meaning ‘equals’, and skelos, meaning ‘leg’. ‘Equilateral’ is derived from the Latin words aequus, meaning ‘equal’, and latus, meaning ‘side’. ‘Equiangular’ is derived from aequus and another Latin word, angulus, meaning ‘corner’. |
LANGUAGE | Students should be able to communicate using the following language: shape, two-dimensional shape (2D shape), triangle, equilateral triangle, isosceles triangle, scalene triangle, right-angled triangle, quadrilateral, parallelogram, rectangle, rhombus, square, trapezium, kite, pentagon, hexagon, octagon, regular shape, irregular shape, features, properties, side, parallel, pair of parallel sides, opposite, length, vertex (vertices), angle, right angle, line (axis) of symmetry, rotational symmetry, order of rotational symmetry, translate, reflect, rotate, enlarge. |
| A ‘feature’ of a shape or object is a generally observable attribute of a shape or object. A ‘property’ of a shape or object is an attribute that requires mathematical knowledge to be identified. |
EXPECTATIONS OF ATTAINMENT
Classify two-dimensional shapes and describe their features | manipulate, identify and name right-angled, equilateral, isosceles and scalene triangles {Literacy} |
| – recognise that a triangle can be both right-angled and isosceles or right-angled and scalene {Reasoning, Critical and creative thinking} | |
| compare and describe features of the sides of equilateral, isosceles and scalene triangles | |
| explore by measurement side and angle properties of equilateral, isosceles and scalene triangles {Critical and creative thinking} | |
| explore by measurement angle properties of squares, rectangles, parallelograms and rhombuses {Critical and creative thinking} | |
| select and classify a two-dimensional shape from a description of its features {Literacy} | |
| – recognise that two-dimensional shapes can be classified in more than one way, e.g. a rhombus can be more simply classified as a parallelogram {Communicating, Reasoning, Critical and creative thinking} | |
| identify and draw regular and irregular two-dimensional shapes from descriptions of their side and angle properties {Literacy} | |
| – use tools such as templates, rulers, set squares and protractors to draw regular and irregular two-dimensional shapes {Communicating, Problem Solving, Critical and creative thinking} | |
| – explain the difference between regular and irregular shapes {Communicating} | |
| – use computer drawing tools to construct a shape from a description of its side and angle properties {Communicating, Problem Solving, Information and communication technology capability} |
Describe translations, reflections and rotations of two-dimensional shapes (ACMMG114) | use the terms ‘translate’, ‘reflect’ and ‘rotate’ to describe the movement of two-dimensional shapes |
| – rotate a graphic or object through a specified angle about a particular point, including by using the rotate function in a computer drawing program {Communicating, Information and communication technology capability} | |
| describe the effect when a two-dimensional shape is translated, reflected or rotated, eg when a vertical arrow is rotated 90°, the resulting arrow is horizontal | |
| – recognise that the properties of shapes do not change when shapes are translated, reflected or rotated {Reasoning, Critical and creative thinking} |
Identify line and rotational symmetries (ACMMG114) | identify and quantify the total number of lines (axes) of symmetry (if any exist) of two-dimensional shapes, including the special quadrilaterals and triangles |
| identify shapes that have rotational symmetry and determine the ‘order’ of rotational symmetry | |
| – construct designs with rotational symmetry, with and without the use of digital technologies {Communicating, Problem Solving, Information and communication technology capability} |
Apply the enlargement transformation to familiar two-dimensional shapes and explore the properties of the resulting image compared with the original (ACMMG115) | make enlargements of two-dimensional shapes, pictures and maps, with and without the use of digital technologies {Information and communication technology capability} |
| – overlay an image with a grid composed of small squares (eg 5 mm by 5 mm) and create an enlargement by drawing the contents of each square onto a grid composed of larger squares (eg 2 cm by 2 cm) {Communicating, Problem Solving, Critical and creative thinking} | |
| – investigate and use functions of digital technologies that allow shapes and images to be enlarged without losing the relative proportions of the image {Problem Solving, Information and communication technology capability} | |
| compare representations of shapes, pictures and maps in different sizes, eg student drawings enlarged on a photocopier | |
| – measure an interval on an original representation and its enlargement to determine how many times larger than the original the enlargement is {Problem Solving, Reasoning, Critical and creative thinking} |
ANGLES
OUTCOME
A student:
MA3-16MG:
measures and constructs angles, and applies angle relationships to find unknown angles
| TEACHING POINTS | A circular protractor calibrated from 0° to 360° may be easier for students to use to measure reflex angles than a semicircular protractor calibrated from 0° to 180°. |
| LANGUAGE | Students should be able to communicate using the following language: angle, arm, vertex, protractor, degree. |
EXPECTATIONS OF ATTAINMENT
Estimate, measure and compare angles using degrees (ACMMG112) | identify the arms and vertex of an angle where both arms are invisible, such as for rotations and rebounds |
| recognise the need for a formal unit for the measurement of angles | |
| record angle measurements using the symbol for degrees (°) {Literacy} | |
| measure angles of up to 360° using a protractor | |
| – explain how a protractor is used to measure an angle {Communicating, Literacy} | |
| – explore and explain how to use a semicircular protractor to measure a reflex angle {Communicating, Reasoning, Critical and creative thinking} | |
| – extend the arms of an angle where necessary to facilitate measurement of the angle using a protractor {Problem Solving, Critical and creative thinking} |
Construct angles using a protractor (ACMMG112) | construct angles of up to 360° using a protractor |
| identify that a right angle is 90°, a straight angle is 180° and an angle of revolution is 360° | |
| identify and describe angle size in degrees for each of the classifications acute, obtuse and reflex | |
| – use the words ‘between’, ‘greater than’ and ‘less than’ to describe angle size in degrees {Communicating, Literacy} | |
| compare the sizes of two or more angles in degrees, eg compare angles in different two-dimensional shapes {Critical and creative thinking} | |
| estimate angles in degrees and check by measuring |
POSITION
OUTCOME
A student:
MA3-17MG:
locates and describes position on maps using a grid-reference system
TEACHING POINTS | In Stage 2, students were introduced to the compass directions north, east, south and west, and north-east, south-east, south-west and north-west. In Stage 3, students are expected to use these compass directions when describing routes between locations on maps. |
| By convention when using grid-reference systems, the horizontal component of direction is named first, followed by the vertical component. This connects with plotting points on the Cartesian plane in Stage 3 Patterns and Algebra, where the horizontal coordinate is recorded first, followed by the vertical coordinate. |
| LANGUAGE | Students should be able to communicate using the following language: position, location, map, plan, street directory, route, grid, grid reference, legend, key, scale, directions, compass, north, east, south, west, north-east, south-east, south-west, north-west. |
EXPECTATIONS OF ATTAINMENT
Use a grid-reference system to describe locations (ACMMG113) | find locations on maps, including maps with legends, given their grid references {Literacy} |
| describe particular locations on grid-referenced maps, including maps with a legend, eg ‘The post office is at E4’ |
Describe routes using landmarks and directional language (ACMMG113) | find a location on a map that is in a given direction from a town or landmark, eg locate a town that is north-east of Broken Hill {Literacy} |
| describe the direction of one location relative to another, eg ‘Darwin is north-west of Sydney’ {Literacy} | |
| follow a sequence of two or more directions, including compass directions, to find and identify a particular location on a map {Literacy} | |
| use a given map to plan and show a route from one location to another, eg draw a possible route to the local park or use an Aboriginal land map to plan a route(Literacy, Aboriginal and Torres Strait Islander histories and cultures} | |
| – use a street directory or online map to find the route to a given location {Problem Solving, Literacy, Information and communication technology capability} | |
| describe a route taken on a map using landmarks and directional language, including compass directions, eg ‘Start at the post office, go west to the supermarket and then go south-west to the park’ {Literacy} |
STATISTICS AND PROBABILITY
DATA
OUTCOME
A student:
MA3-18SP:
uses appropriate methods to collect data and constructs, interprets and evaluates data displays, including dot plots, line graphs and two-way tables
TEACHING POINTS | Column graphs are useful in recording categorical data, including results obtained from simple probability experiments. |
| A scale of many-to-one correspondence in a column graph or line graph means that one unit is used to represent more than one of what is being counted or measured, eg 1 cm on the vertical axis used to represent 20 cm of body height. | |
| Line graphs should only be used where meaning can be attached to the points on the line between plotted points, eg temperature readings over time. | |
| Dot plots are an alternative to a column graph when there are only a small number of data values. Each value is recorded as a dot so that the frequencies for each of the values can be counted easily. | |
| Students need to be provided with opportunities to discuss what information can be drawn from various data displays. Advantages and disadvantages of different representations of the same data should be explicitly taught. | |
| Categorical data can be separated into distinct groups, eg colour, gender, blood type. Numerical data is expressed as numbers and obtained by counting, or by measurement of a physical attribute, eg the number of students in a class (count) or the heights of students in a class (measurement). |
| LANGUAGE | Students should be able to communicate using the following language: data, survey, category, display, tabulate, table, column graph, vertical columns, horizontal bars, equal spacing, title, scale, vertical axis, horizontal axis, axes, line graph, dot plots, spreadsheet. |
Expectations of Attainment
Pose questions and collect categorical or numerical data by observation or survey (ACMSP118) | pose and refine questions to construct a survey to obtain categorical and numerical data about a matter of interest {Difference and diversity} |
| collect categorical and numerical data through observation or by conducting surveys, eg observe the number of a particular type of insect in one square metre of the playground over time {Sustainability, Difference and diversity} |
Construct displays, including column graphs, dot plots and tables, appropriate for data type, with and without the use of digital technologies (ACMSP119) | tabulate collected data, including numerical data, with and without the use of digital technologies such as spreadsheets {Information and communication technology capability} |
| construct column and line graphs of numerical data using a scale of many-to-one correspondence, with and without the use of digital technologies | |
| – name and label the horizontal and vertical axes when constructing graphs {Communicating, Literacy} | |
| – choose an appropriate title to describe the data represented in a data display {Communicating, Literacy} | |
| – determine an appropriate scale of many-to-one correspondence to represent the data in a data display {Reasoning} | |
| – mark equal spaces on the axes when constructing graphs, and use the scale to label the markers {Communicating, Literacy} | |
| construct dot plots for numerical data, eg the number of siblings of each student in the class {Information and communication technology capability} | |
| consider the data type to determine and draw the most appropriate display(s), such as column graphs, dot plots and line graphs | |
| – discuss and justify the choice of data display used {Communicating, Reasoning, Critical and creative thinking} | |
| – recognise that line graphs are used to represent data that demonstrates continuous change, eg hourly temperature {Communicating, Sustainability} | |
| – recognise which types of data display are most appropriate to represent categorical data {Communicating} |
Describe and interpret different data sets in context (ACMSP120) | interpret line graphs using the scales on the axes {Literacy} |
| describe and interpret data presented in tables, dot plots, column graphs and line graphs, eg ‘The graph shows that the heights of all children in the class are between 125 cm and 154 cm’ {Literacy} | |
| – determine the total number of data values represented in dot plots and column graphs, eg find the number of students in the class from a display representing the heights of all children in the class {Problem Solving, Reasoning} | |
| – identify and describe relationships that can be observed in data displays, eg ‘There are four times as many children in Year 5 whose favourite food is noodles compared to children whose favourite food is chicken’ {Communicating, Reasoning, Literacy} | |
| – use information presented in data displays to aid decision making, eg decide how many of each soft drink to buy for a school fundraising activity by collecting and graphing data about favourite soft drinks for the year group or school {Reasoning, Critical and creative thinking} |
CHANCE
OUTCOME
A student:
MA3-19SP:
conducts chance experiments and assigns probabilities as values between 0 and 1 to describe their outcomes
TEACHING POINTS | Students will need some prior experience in ordering fractions and decimals on a number line from 0 to 1. |
| The probability of chance events occurring can be ordered on a scale from 0 to 1. A probability of 0 describes the probability of an event that is impossible. A probability of 1 describes the probability of an event that is certain. Events with an equal likelihood of occurring or not occurring can be described as having a probability of 1/2 (or 0.5 or 50%). Other expressions of probability fall between 0 and 1, eg events described as ‘unlikely’ will have a numerical value somewhere between 0 and 1/2 (or 0.5 or 50%). | |
| The sum of the probabilities of the outcomes of any chance experiment is equal to 1. This can be demonstrated by adding the probabilities of all of the outcomes of a chance experiment, such as rolling a die. |
LANGUAGE | Students should be able to communicate using the following language: chance, event, likelihood, certain, possible, likely, unlikely, impossible, experiment, outcome, probability. |
| The probability of an outcome is the value (between 0 and 1) used to describe the chance that the outcome will occur. | |
| A list of all of the outcomes for a chance experiment is known as the ‘sample space’; however, this term is not introduced until Stage 4. |
EXPECTATIONS OF ATTAINMENT
List outcomes of chance experiments involving equally likely outcomes and represent probabilities of those outcomes using fractions (ACMSP116) | use the term ‘probability’ to describe the numerical value that represents the likelihood of an outcome of a chance experiment {Literacy} |
| recognise that outcomes are described as ‘equally likely’ when any one outcome has the same chance of occurring as any other outcome {Literacy} | |
| list all outcomes in chance experiments where each outcome is equally likely to occur | |
| represent probabilities of outcomes of chance experiments using fractions, eg for one throw of a standard six-sided die or for one spin of an eight-sector spinner | |
| – determine the likelihood of winning simple games by considering the number of possible outcomes, eg in a ‘rock-paper-scissors’ game {Problem Solving, Reasoning, Information and communication technology capability, Critical and creative thinking} |
Recognise that probabilities range from 0 to 1 (ACMSP117) | establish that the sum of the probabilities of the outcomes of any chance experiment is equal to 1 |
| order commonly used chance words on an interval from zero (‘impossible’) to one (‘certain’), eg ‘equally likely’ would be placed at 1/2 (or 0.5) {Literacy} | |
| – describe events that are impossible and events that are certain {Communicating, Literacy, Critical and creative thinking} | |
| – describe the likelihood of a variety of events as being more or less than a half (or 0.5) and order the events on an interval {Communicating} |